What is a Slope (Gradient)?
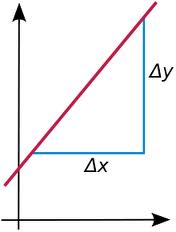
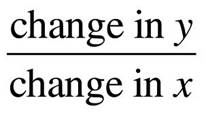
The slope of a line is a number that measures its "steepness". It is the change in y for a unit change in x along the line.
The slope of a line is generally denoted by m.
Thus,
m = tan θ Since a line parallel to x – axis makes an angle of 0° with x – axis, therefore its slope is tan 0° = 0.
Since a line parallel to x – axis makes an angle of 0° with x – axis, therefore its slope is tan 0° = 0.
A line parallel to y – axis, perpendicular to x – axis makes an angle of 90 with x – axis, so its slope is tan 90° = ∞. Also, the slope of a line equally inclined with axes is 1 or -1 as it makes 45° or 135° with x – axis.
The angle of inclination of a line with the positive direction of x – axis in anticlockwise sense always lies between 0° and 180°.
Slope of a line in terms of coordinates of any two points on it
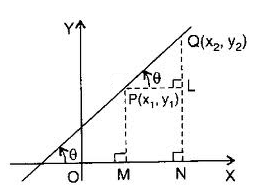
Let P (x1, y1) and Q (x2, y2) be two points on a line making an angle θ with the positive direction of x – axis. Draw PM, QN perpendiculars on x – axis and PL perpendicular on QN.
Then, PL = MN = ON – OM = x2 – x1
and QL = ON – LN = QN – PM = y2 – y1
In ΔPQL, tan θ = QL/PL = (y2 – y1)/(x2 – x1)
Thus, if (x1, y1) and (x2, y2) are coordinates of any two points on a line, then its slope is
m = (y2 – y1)/(x2 – x1)
m = Difference of ordinates
Difference of abscissae
or, m = Vertical Step
Horizontal Step
Angle between two lines
The angle θ between the lines having slopes m1 and m2 is given by
tan θ = + m2 – m1
1 + m1m2
Slope (Gradient) of Parallel lines
If two lines of slopes m1 and m2 are parallel, then the angle θ between them is 0°.
tan θ = tan 0° = 0
m2 – m1 = 0
1 + m1m2
m2 = m1
Thus, when two lines are parallel, their slopes are equal.
Slope (Gradient) of Perpendicular lines
If two lines of slope m1 and m2 are perpendicular, then the angle θ between them is of 90°
cot θ = 1 + m1m2
m2 – m1
0 = 1 + m1m2
m1m2 = -1
Thus, when two lines are perpendicular, the product of their slopes is -1. If m is the slope of a line, then the slope of a line perpendicular to it is - (1/m).
Now try it yourself! Should you still need any help, click here to schedule live online session with e Tutor!
About eAge Tutoring :
eAgeTutor.com is the premium online tutoring provider. Using materials developed by highly qualified educators and leading content developers, a team of top-notch software experts, and a group of passionate educators, eAgeTutor works to ensure the success and satisfaction of all of its students.
Contact us today to learn more about our guaranteed results and discuss how we can help make the dreams of the student in your life come true!