Algebraic Methods of Solving a Pair of Linear Equations

Created: Tuesday, 19 July 2011 08:55 | Published: Tuesday, 19 July 2011 08:55 | Written by Super User | Print

What is a linear equation?

The pair of the linear equation is in the following form-

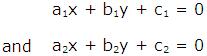
linearequationalgebraic1

The most commonly used algebraic methods of solving a pair of linear equations in two variables are –

a) Substitution method

b) Elimination method

c) Cross Multiplication method

Let’s discuss these methods one by one:

Substitution Method

Here are the steps which we follow while solving a pair linear equations:

Step I – Obtain the two equations. Let the equations be

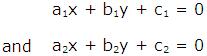linearequationalgebraic1 ........................(i)

........................(ii)

Step II – Choose either of the two equations, say (i), and find the value of one variable, say y, in terms of the other, i.e. x.

Step III – Substitute the value of y, obtained in step II, in other equation i.e. (ii) to get an equation in x.

Step IV – Solve the equation obtained in step III to get the value of x.

Step V – Substitute the value of x obtained in step IV in the expression for y in terms of x obtained in step II to get the value of y.

Step VI – The values of x and y obtained in steps IV and V respectively constitute the solution of the given system of two linear equations.

Example: Solve the following system of equations by using the method of substitution:

3x – 5y = -1

x – y = -1

Let, 3x – 5y = -1 … (i)

and x – y = -1 … (ii)

From (ii), we get y = x + 1

Substituting y = x + 1 in (i), we get

3x – 5(x + 1) = -1

-2x – 5 = -1

-2x = 4

x = -2

Putting x = -2 in y = x + 1 we get y = -1

Hence, the solution of the given system of equations is x = -2 and y = -1.

Try these questions now:

1. Solve the following system of equations by using the method of substitution:

x + 2y = -1
2x – 3y = 12

(Answer: x = 3 and y = -2)

2. Solve the following system of equations by using the method of substitution:

2x + 3y = 9
3x + 4y = 5

(Answer: x = -21 and y = 17)

Now try it yourself! Should you still need any help, click here to schedule live online session with e Tutor!

About eAge Tutoring :

eAgeTutor.com is the premium online tutoring provider. Using materials developed by highly qualified educators and leading content developers, a team of top-notch software experts, and a group of passionate educators, eAgeTutor works to ensure the success and satisfaction of all of its students.

Contact us today to learn more about our guaranteed results and discuss how we can help make the dreams of the student in your life come true!

Reference Links :

Category: ROOT