Addition and Subtraction of Decimals
 In order to add decimals or subtract decimals, we may use the following steps:
In order to add decimals or subtract decimals, we may use the following steps:
• Convert the given decimals to like decimals.
• Write the decimals in columns with their decimal points directly below each other so that tenths come under tenths, hundredths come under hundredths and so on.
• Add or subtract as we add or subtract whole numbers.
• Place the decimal point, in the answer, directly below the other decimal points.
For example, Add 15.44, 7.524 and 25
Converting the given decimals to like decimals, we have 15.440, 7.524. 25.000.
Now,
15.440
+7.524
+ 25.000
![]()
47.964
Example 2 – Subtract: 9.756 – 6.28
We proceed the same way as we did for addition, converting the given decimals to like decimals, we have 9.756 and 6.280.
Multiplication of decimals
Stages in multiplying decimals
• Multiplication of a decimal by 10, 100, 1000.
• Multiplication of a decimal by a whole number.
• Multiplication of a decimal by another decimal.
Multiplication of a decimal by 10, 100, 1000
We follow the following rules to multiply a decimal by 10, 100, 1000:
• On multiplying a decimal by 10, the decimal point is shifted to the right by one place.
• On multiplying a decimal by 100, the decimal point is shifted to the right by two places.
• On multiplying a decimal by 1000, the decimal point is shifted to the right by three places, and so on.
For example, find the product – 27.05 x 10
27.05 x 10 = 270.5 [Shifting the decimal point by one place]
Example 2 – Find the product: 27.05 x 100
27.05 x 100 = 2705.00 [Shifting the decimal point by two places]
Example 3 – Find the product: 27.05 x 1000
27.05 x 1000 = 27050.00 [Shifting the decimal point by three places and if get short of the digits, we add zero as done in this example]
Multiply a decimal by a whole number
Multiply the decimal without the decimal point by the given whole number.
• Mark the decimal point in the product to have as many places of decimal as are there in the given decimal.
For example, find the product – 3.25 x 12
325 x 12 = 3900
3.25 x 12 = 39.00
Multiplication of a decimal by another decimal
In order to multiply a decimal by another decimal, we follow the following steps:
• Multiply the two decimals without decimal point just like whole numbers.
• Insert the decimal point in the product by counting as many places from the right to left as sum of the number of decimal places of the given decimals.
For example, find the product - 9.2 x 6.07
We have,
92 x 607 = 55844
Since the sum of the decimal places in the given decimals is 1 + 2 = 3.
So, the product must contain 3 places of decimals.
Hence, 9.2 x 6.07 = 55.844
Division of decimals
Stages in dividing decimals
• Dividing a decimal by 10, 100, 1000.
• Dividing a decimal by a whole number.
• Dividing a decimal by another decimal.
Division of a decimal by 10, 100, 1000
We follow the following rules to divide a decimal by 10, 100, 1000 :
• When a decimal is divided by 10, the decimal point is shifted to the left by one place.
• When a decimal is divided by 100, the decimal point is shifted to the left by two places.
• When a decimal is divided by 1000, the decimal point is shifted to the left by three places, and so on.
For example, divide - 99.08 ÷ 10
99.08 ÷ 10 = 9.908 [Shifting the decimal point to the left by one place]
Example 2 – Divide - 99.08 ÷ 100
99.08 ÷ 100 = 0.9908 [Shifting the decimal point to the left by two places]
Example 3 – Divide - 99.08 ÷ 1000
99.08 ÷ 1000 = 0.09908 [Shifting the decimal point to the left by three places and if get short of the digits, we add zero as done in this example]
Divide a decimal by a whole number
• Check the whole number part of the dividend.
• If the whole number part of the dividend is less than the divisor, then place a 0 in the ones place in the quotient. Otherwise, go to next step.
• Divide the whole number part of the dividend.
• Place the decimal point to the right of one’s place in the quotient obtained in the very first step.
• Divide the decimal part of the dividend by the divisor. If the digits of the dividend are exhausted, then place zeros to the right of dividend and remainder each time and continue the process.
For example, divide 93.45 by 15
We have, 
Division of a decimal by another decimal
In order to divide a decimal by another decimal, we follow the following steps:
• Multiply the dividend and divisor by 10 or 100 or 1000 to convert the divisor into a whole number.
• Divide the new dividend by the whole number obtained in previous step.
For example, divide 3.28 by 0.4
We have, 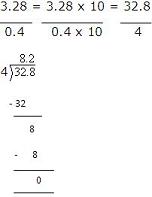
![]()
Now try it yourself! Should you still need any help, click here to schedule live online session with e Tutor!
![]()
About eAge Tutoring:
eAgeTutor.com is the premium online tutoring provider. Using materials developed by highly qualified educators and leading content developers, a team of top-notch software experts, and a group of passionate educators, eAgeTutor works to ensure the success and satisfaction of all of its students.
Contact us today to learn more about our tutoring programs and discuss how we can help make the dreams of the student in your life come true!