Interference and the Wave Nature of Light
What is Interference?
Interference is the superposition of two (or more) waves of the same kind passing the same point in space at the same time. If the waves are in the same phase, e.g. crest on crest, their amplitudes will combin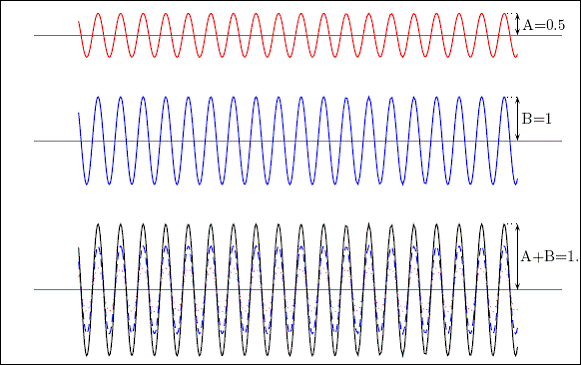 e to produce a strong wave. This is called “constructive interference.” If the waves are out of phase, e.g. if the crests of one are superposed on the troughs of another, we get “destructive interference.”
e to produce a strong wave. This is called “constructive interference.” If the waves are out of phase, e.g. if the crests of one are superposed on the troughs of another, we get “destructive interference.”
If two identical (same wavelength, amplitude and frequency) waves are both trying to form a peak then they will achieve the sum of their efforts. The resulting motion will be a peak that has a height which is the sum of the heights of the two waves. If two waves are both trying to form a trough at the same place and time then a deeper trough will be formed, and the depth of this trough will be the sum of the depths of the two waves.
CONDITIONS FOR INTERFERENCE
- The two sources of light should emit continuous waves of the same wavelength and same time period. I.e., the sources should have phase coherence.
- The two sources of light should be very close to each other.
- The waves emitted by the two sources should either have zero phase difference or no phase difference.
Suppose two waves, y1 and y2, have nearly the same wavelength and phase (i.e., the maxima occur at nearly the same time and place). Superposition of these waves results in a wave (y1 + y2) of almost twice the amplitude of the individual waves. See the first figure below. This is called constructive interference. If the maximum of one wave is near the minimum of the other wave, the resultant (y1 + y2) has almost no amplitude, as shown in the second figure below. This is called destructive interference.
Conditions for Constructive Interference
In constructive interference, the amplitude of the resultant wave at a given position or time is greater than the amplitude of either individual wave.
For constructive interference, the path difference between two waves is mλ
i.e. path difference = mλ
or path difference = 0, l, 2λ, 3λ, 4λ, ..........
where m = order = 0, +_1, +_2, +_3,…..
 Conditions for Destructive Interference
Conditions for Destructive Interference
If the path difference between two light waves is (m+1/2)λ, then the interference between them is destructive.
Path difference = (m+1/2)λ
i.e. path difference = 1/2λ, 3/2λ, 5/2λ, ...........
where m = order = 0, +_1, +_2, +_3,…..
***
Want to know more about interference? Click here to schedule a live session with an eAge eTutor!
About eAge Tutoring:
eAgeTutor.com is the premium online tutoring provider. Using materials developed by highly qualified educators and leading content developers, a team of top-notch software experts, and a group of passionate educators, eAgeTutor works to ensure the success and satisfaction of all of its students.
Contact us today to learn more about our guaranteed results and discuss how we can help make the dreams of the student in your life come true!
