Introduction to Isothermal Processes
An isothermal process is the process in thermodynamics in which temperature is kept constant. A gas confined by a piston in a cylinder can again provide an example of this, only this time the gas is not heated or cooled, and instead the piston is slowly moved so that the gas expands or is compressed. The temperature is maintained at a constant value by putting the system in contact with a constant-temperature reservoir (the thermodynamic definition of a reservoir is something large enough that it can transfer heat into or out of a system without changing temperature). In an isothermal process, the temperature stays constant, so the pressure and volume are inversely proportional to one another.What is an Isothermal process?
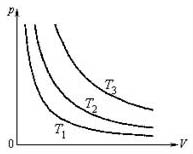 An isothermal process is a thermodynamic process in which the temperature of a system remains constant; ΔT = 0. This process occurs when a system is in contact with an outside thermal reservoir, and the system changes slowly enough to allow it to adjust to the temperature of the reservoir. The opposite extreme in which a system exchanges no heat with its surroundings is known as an adiabatic process. Isothermal processes are represented at different temperatures T through a family of hyperbolas p ~ 1 / V, which are called isotherms. The coefficient of proportionality in this equation increases with increasing temperature.
An isothermal process is a thermodynamic process in which the temperature of a system remains constant; ΔT = 0. This process occurs when a system is in contact with an outside thermal reservoir, and the system changes slowly enough to allow it to adjust to the temperature of the reservoir. The opposite extreme in which a system exchanges no heat with its surroundings is known as an adiabatic process. Isothermal processes are represented at different temperatures T through a family of hyperbolas p ~ 1 / V, which are called isotherms. The coefficient of proportionality in this equation increases with increasing temperature.The family of isotherms in the plane (p, V). T 3> T 2> T 1
Reversible and Irreversible process
A process that, once having taken place, can be reversed and in doing so leaves no change in either the system or the surroundings. Net work and net heat transfer must be zero A reversible process is an ideal that we never achieve – all processes are irreversible. They are standards to which we can compare different processes. A Carnot cycle to which we compare all other cycles. Irreversibility are what cause a process to be irreversible. External irreversibilities occur outside the system we are looking at. Internal irreversibilities occur inside the system we are looking at. A totally reversible system is internally & externally reversible. Heat transfer through a finite temperature difference, mixing of different substances is some examples of irreversible process.
Explanation
Consider a cylinder of non-conducting walls with a good heat conducting base. The cylinder is fitted with a frictionless piston. An ideal gas is enclosed in the cylinder. In the first stage, pressure on the piston is increased and the cylinder is placed on a cold body. Due to compression, the temperature of the system increases but at the same time DQ amount of heat is removed from the system and the temperature of the system is maintained.
According to the first law of thermodynamics:
DQ = DU+ DW
Since temperature is constant, there is no change in the system’s internal energy, i.e., DU = 0
As the work is done on the system, therefore, DW is negative,
DQ = 0+ (-DW)
DQ = -DW
 This means that, during an isothermal process, all heat accepted by the system from its surroundings must have its energy entirely converted to work which it then performs on the surroundings, so that all the energy which comes into the system then comes right back out of the system. This way, the internal energy (and thus the temperature) of the system remains constant.
This means that, during an isothermal process, all heat accepted by the system from its surroundings must have its energy entirely converted to work which it then performs on the surroundings, so that all the energy which comes into the system then comes right back out of the system. This way, the internal energy (and thus the temperature) of the system remains constant.
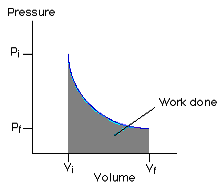
In an isothermal process, the temperature stays constant, so pressure and volume are inversely proportional to one another. The P-V graph for an isothermal process is as follows:
P-V Expansion at constant Temperature
The internal energy of an ideal gas is proportional to the temperature, so if the temperature is kept fixed the internal energy does not change. The first law, which deals with changes in the internal energy, thus becomes 0 = Q - W, so Q = W. If the system does work, the energy comes from heat flowing into the system from the reservoir; if work is done on the system, heat flows out of the system to the reservoir.
Want to know more about isothermal processes? Click here to schedule a live session with an eAge eTutor!
About eAge Tutoring:
eAgeTutor.com is the premium online tutoring provider. Using materials developed by highly qualified educators and leading content developers, a team of top-notch software experts, and a group of passionate educators, eAgeTutor works to ensure the success and satisfaction of all of its students.
Contact us today to learn more about our guaranteed results and discuss how we can help make the dreams of the student in your life come true!