Introduction to Heat engines
Any machine or device whose main function is to convert some percentage of available heat into useful work is called a heat engine. To act practically as a continuous operatio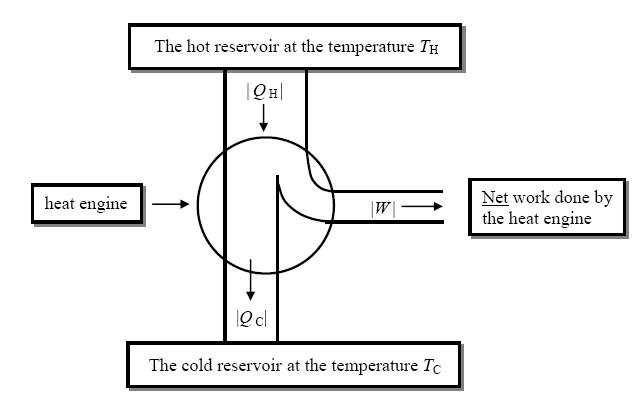 n (as in an automobile engine), it should always run in cycles so that its function can be repeated many times.
n (as in an automobile engine), it should always run in cycles so that its function can be repeated many times.
Heat Engine
In each cycle, a heat engine will take in a certain amount of heat, QH, from a hot reservoir (i.e., a large source or sink of heat), convert a fraction f of it into useful work (which can then be converted into any other form of energy with, in principle at least, 100% efficiency), and dump the remaining heat into a colder reservoir (such as the air, or the water in a lake, river, ocean, etc.). If f were 1/1, there would be no remaining heat to dump out to a cold reservoir. The conversion of heat to work would then have 100% efficiency. Unfortunately, as we shall see, this is impossible. We can represent a heat engine by the schematic diagram above.
Heat Engine Processes
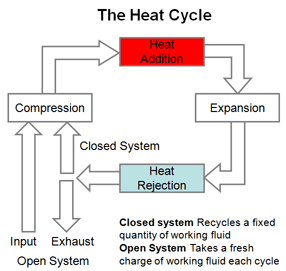 The heat cycle involves three or more basic thermodynamic basic processes, and typically four, to transform the state of the working fluid and return it to its original state. These are; compression, heat addition, expansion, and heat rejection. Each of these processes can be carried out under one or more of the following conditions:
The heat cycle involves three or more basic thermodynamic basic processes, and typically four, to transform the state of the working fluid and return it to its original state. These are; compression, heat addition, expansion, and heat rejection. Each of these processes can be carried out under one or more of the following conditions:
Isothermal -- At constant temperature, maintained with heat added or removed from a heat source or sink.
Isobaric -- At constant pressure.
Isometric / Isochoric / Iso-volumetric -- At constant volume.
Adiabatic -- At constant temperature. No heat is added or removed from the system. No work is done.
Isentropic At constant entropy. Reversible adiabatic conditions. No heat is added or lost, and no work is done.
Work Done During One Heat Cycle
The mechanical work taken from a system is given by the equation:
W = - ∫P.dV (Integral around one complete cycle)
From the PV diagram, this integral is equivalent to the area enclosed by the curve.
Heat Engine Efficiency
We define the efficiency e of a heat engine as:
Efficiency Notes
It is important to know that heat | Q H | is taken out of the hot reservoir by the engine, whereas heat | Q C | is dumped into the cold reservoir by the engine. Finally work |W | is done by the engine. Thus from the point of view of the working substance of the engine, Q H should be positive, QC should actually be negative, and W should be positive, since any heat flowing into a system is positive, and any work done by the system is positive.
The highest possible value for e is 1/1. But if e were 1/1, we would have
| Q C | = 0, with | Q H | > 0, and there would be no heat dumped into any cold reservoir, or | Q H | = ∞, with | Q C | zero or finite. We shall see that these situations are impossible. As a matter of fact, we shall see that the highest possible value for e is the Carnot efficiency (1 T C / T H ), which is less than 1/1, unless T C is absolute zero, or T H is infinity, or both, which is impossible!
***
Want to know more about heat engines? Click here to schedule a live session with an eAge eTutor!
About eAge Tutoring:
eAgeTutor.com is the premium online tutoring provider. Using materials developed by highly qualified educators and leading content developers, a team of top-notch software experts, and a group of passionate educators, eAgeTutor works to ensure the success and satisfaction of all of its students.
Contact us today to learn more about our guaranteed results and discuss how we can help make the dreams of the student in your life come true!
