Introduction to Kinetic Theory of Gases
 A Scottish botanist, Robert Brown, first suggested that gases were in a state of random motion. His model of the physics of gases, which describes the behavior of an ideal gas, portrays them much like a group of billiard balls moving on a billiard table. He observed that pollen particles seem to jiggle about for no apparent reason.
A Scottish botanist, Robert Brown, first suggested that gases were in a state of random motion. His model of the physics of gases, which describes the behavior of an ideal gas, portrays them much like a group of billiard balls moving on a billiard table. He observed that pollen particles seem to jiggle about for no apparent reason.We see the same thing when observing smoke particles under a microscope. The random jerky movement of the particles is called Brownian motion and is due to their continuous and random bombardment by air molecules. The work of Einstein, Maxwell, and Boltzmann gave us the kinetic theory, as we know it today.
Temperature and pressure are macroscopic properties of gases. These properties are related to molecular motion, which is a microscopic phenomenon. The kinetic theory of gases correlates macroscopic properties and microscopic phenomena. Kinetics means the study of motion, and in this case, the motion of gas molecules.
Main Postulates of the Kinetic Molecular Theory of Gases:
- A gas consists of very small microscopic particles called “molecules.” Depending on the nature of the gas, each gas molecule can consist of an atom or group of atoms. Molecules are in continuous motion.
- All the molecules of a gas are in a stable state and are considered identical.
- Any finite volume of a gas consists of a very large number of molecules.
- At S.T.P. there are 3 x 1025 molecules in a cubic meter.
- Compared to their own dimensions, the molecules are wide apart from each other.
- The diameter of a molecule is about 3 x 10-10 meters.
- Gas molecules move in straight lines in all possible directions (i.e., they randomly move) at various speeds.
- Gas molecules collide with each other and with the walls of containers. Their collisions are perfectly elastic in nature.
- When gas molecules collide with the walls of a container, they transfer their momentum, which appears as the pressure of gas.
- The molecules of an ideal gas exert no force of attraction or repulsion on one another except during collision.
- The average kinetic energy of gas molecules is directly proportional to absolute temperature.
- At a given temperature, the molecules of all gases have the same kinetic energy.
- Newtonian mechanics is applicable to molecular motion.
Temperature
The kinetic theory explains why temperature should be a measure of the average kinetic energy of molecules. According to the kinetic theory, any given molecule has a certain mass, m; a certain velocity, v; and a kinetic energy of 1/ 2 mv2. As we said, molecules in any system move at a wide variety of different velocities, but the average of these velocities reflects the total amount of energy in that system.
We know from experience that substances are solids at lower temperatures, while liquids and gases are substances at higher temperatures. This accords with our definition of temperature as average kinetic energy; because the molecules in gases and liquids have more freedom of movement, they have a higher average velocity.
Pressure
In the kinetic-molecular theory of gases, pressure is the force exerted against the wall of a container by the continual collision of molecules against it. In physics, pressure, P, is the measure of the force exerted over a certain area. We generally say that something exerts a lot of pressure on an object if it exerts a great amount of force on that object, and if that force is exerted over a small area. Mathematically:
Pressure is measured in units of pascals (Pa), where 1 Pa = 1 N/m2.
Pressure comes into play whenever force is exerted on a certain area, but is a particularly important characteristic of gases. Molecules are assumed to rebound elastically, with no kinetic energy lost in perpendicular collision. Therefore, ∆v = v - (-v) = 2v (see figure below). If a molecule is moving perpendicular to a wall, then it will strike the opposite parallel wall, rebound, and return to strike the original wall again. If the length of the container or distance between the two walls is the path length l, then the time between two successive collisions on the same wall will be ∆t = 2l/v. Therefore, the continuous force that a molecule moving perpendicular to a wall exerts is:
 Change in momentum as a particle hits a wall
Change in momentum as a particle hits a wallThe molecules in a sample of gas are not, of course, all moving perpendicularly to a wall. However, the components of their actual movement can be imagined to be along the three mutually perpendicular x, y, and z axes. If the number of molecules moving randomly, N, is large, then on the average, one-third can be assumed to exert their force along each of the three perpendicular axes. The square of the average velocity along each axis, v2(x), v2(y), or v2(z), will then be one-third of the square of the average total velocity v2:
v2(x)= v2(y)= v2(z)= v2/3
The average or mean of the square of the total velocity can replace the square of the perpendicular velocity. Therefore, for a large number of molecules N
F= (N/3) mv2/l
Consequently, the pressure will be given by
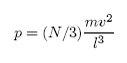
(since P = F/A)
Want to know more about the kinetic theory of gases? Click here to schedule a live session with an eAge eTutor!
About eAge online Tutoring
About eAge online Tutoring
eAgeTutor.com is the premium online tutoring provider. Using materials developed by highly qualified educators and leading content developers, a team of top-notch software experts, and a group of passionate educators, eAgeTutor works to ensure the success and satisfaction of all of its students.
Contact us today to learn more about our guaranteed results and discuss how we can help make the dreams of the student in your life come true!