Degree of freedom

Created: Tuesday, 30 August 2011 06:29 | Published: Tuesday, 30 August 2011 06:29 | Written by Super User | Print

Introduction to Degree of freedom

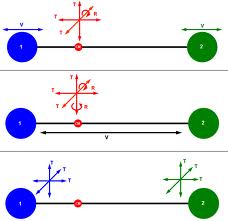The number of independent directions in which a system (or gas molecule) can move, are called the number of degrees of freedom of that system or molecule.

The number of degree of freedom is required to express the position, energy and motion of a system.

If a particle in motion is confined to a straight line, it has only one translational degree of freedom, while if the same particle is confined to move in a plane, it will have two translational degrees of freedom.

If the particle is free to move in space, it will have three translational degrees of freedom.

Types of Energy

A gas molecule can have following types of energies:

(a) Translational kinetic energy

(b) Rotational kinetic energy

Monatomic gases

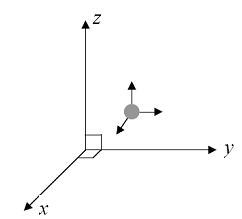Figuring out the degree of freedom for monatomic gases is simple because internal energy is stored only in the translational motion of the atoms. That is, the atoms move as a point-like body and can move in three independent directions.

For a monatomic gas, there are three translational degrees of freedom corresponding to the three axes of movement.

As its rotational moment of inertia is very low (due to small atomic radius), the degree of freedom associated with rotation does not make an appreciable contribution to the kinetic energy. Therefore, a monatomic gas has 3 degrees of freedom.

Degree of freedom f = 3 (all translational)

Diatomic gases

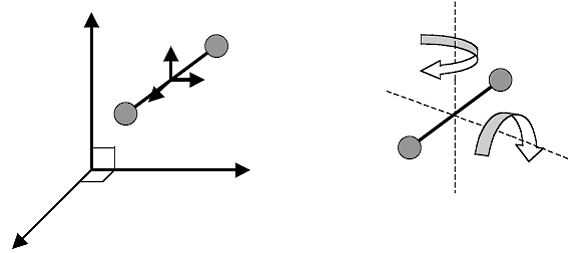For diatomic and polyatomic molecules, rotational motion is significant.

In these cases both translational and rotational motion can contribute to the heat capacity:

For a diatomic gas, in addition to the three degrees for translatory motion, there are two degrees of rotatory motion around axes perpendicular to the bond between the atoms.

Degree of freedom, f = 5 (3 translational +2 rotational) at room temperature f = 7 (3 translational+2 rotational+2 vibrational) at high temperature

Polyatomic gas

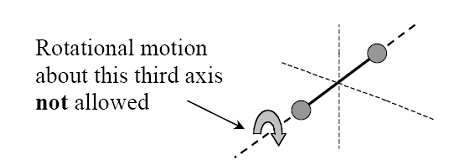A polyatomic (non-linear) molecule (such as NH3) can rotate about any of three co-ordinate axes. Hence it has 6 degrees of freedom, 3 translational and 3 rotational. At room temperature, a polyatomic gas molecule has vibrational energy greater than that of a diatomic gas. The atoms within the molecule may also vibrate with respect to each other at high temperature. In such cases, the molecule will have an additional degree of freedom, due to vibrational motion.

The vibrational motion of a molecule can contribute as much as to two further degrees of freedom. Vibrational motion is not allowed with diatomic molecules but can occur with polyatomic molecules

Degree of freedom, f = 6 (3 translational +3 rotational) at room temperature

f = 8 (3 translational+3 rotational+2 vibrational) at high temperature

Want to know more about degrees of freedom? Click here to schedule a live session with an eAge eTutor!

About eAge online Tutoring

eAgeTutor.com is the premium online tutoring provider. Using materials developed by highly qualified educators and leading content developers, a team of top-notch software experts, and a group of passionate educators, eAgeTutor works to ensure the success and satisfaction of all of its students.

Contact us today to learn more about our guaranteed results and discuss how we can help make the dreams of the student in your life come true!

Reference links

Category: ROOT