What is an angle?
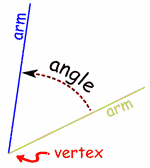 An angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.
An angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.
We can classify angles according to their size and position.
Angles according to their size
The following are the types of angles according to their size:
1. Acute Angle
2. Obtuse Angle
3. Right Angle
4. Straight Angle
5. Reflex Angle
6. Revolution
7. Complementary Angles
8. Supplementary Angles
Let’s discuss each of the angles in detail:
Acute Angle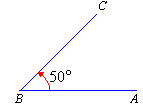
If an angle is greater than 0 degree but less than 90 degrees, then we call that angle as acute angle.
The following is an acute angle.
Example: 30 degrees, 70 degrees etc. are acute angle
Obtuse Angle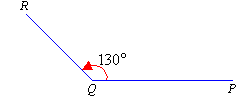
An angle whose measure is greater than 90 degrees but less than 180 degrees is called an obtuse angle.
Thus, it is between 90 degrees and 180 degrees. The following is an obtuse angle.
Example: 150 degrees, 120 degrees etc.
Right Angle
An angle whose measure is 90 degrees is called a right angle.
A right angle is marked on the diagram as a small square.
Straight angle
An angle whose measure is 180 degrees. A straight angle looks like a straight line.
The following is a straight angle.![]()
Reflex angle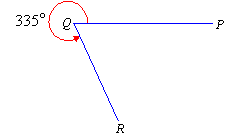
An angle whose measure is greater than 180 degrees but less than 360 degrees.
The following is a reflex angle.
Revolution
A revolution is an angle that equals exactly 360º.![]()
Complementary an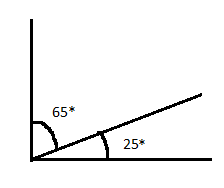 gles
gles
If sum of two angles are 90 degree then they are complementary angles.
For example: Angle measure of 65° and 25° are complementary angles.
As, 65 + 25 = 90°
But angle 65 and angle 25 do not have to be adjacent to be complementary as long as they add up to 90 degrees.
Supplementary angles
If sum of two angles are 180 degree then they are supplementary angles.
Angle measure of 145° and 35° are supplementary angles.
As, 145 + 35= 180
Try This:
1. What is the measure of a right angle?
2. Name the following angles:
a) 160 degrees
b) 75 degrees
c) Sum of angles 110 and 70
Answers
1. 90 degree angle
2. a) Obtuse angle
b) Acute angle
c) Supplementary angles
Angles according to their position
The following are the types of angles according to their position:
1. Adjacent Angles
2. Vertically opposite Angles
3. Angles between parallel lines:
3. (a) Interior Angles
3. (b) Exterior Angles
3. (c) Alternate Interior Angles
3. (d) Alternate Exterior Angles
3. (e) Corresponding Angles
Let’s discuss each of them in detail:
Adjacent Angle s
s
Angle with a common vertex and one common side.
In the following figure ∠ 1 and ∠ 2, are adjacent angles.
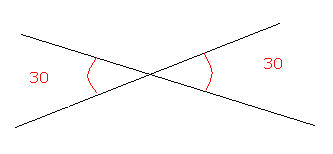
Vertically Opposite Angles
Angles that have a common vertex and whose sides are formed by the same lines. Vertically Opposite angles are always equal.
The following figure represents vertically opposite angles.

Angle formed by Parallel lines
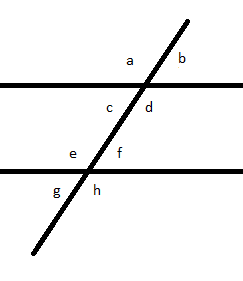
When two parallel lines are crossed by a third line (Transversal), 8 angles are formed.
Take a look at the following figure
We will now discuss the angles formed by the parallel lines:

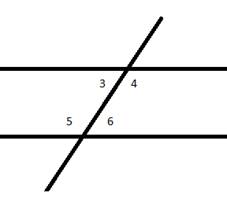
Interior Angles
In the adjoining figure, ∠3, ∠4, ∠5, ∠6 are interior angles.

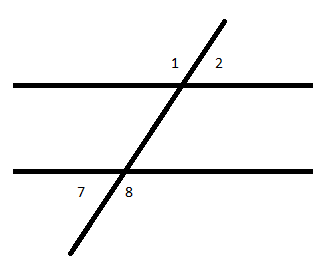
Exterior Angles
In the adjoining figure, ∠1, ∠2, ∠7, ∠8 are exterior angles.
Alternate Interior Angles
Pairs of interior angles on opposite sides of the transversal are Alternate Interior Angles.
∠3 and ∠6are alternate interior angles.
∠4 and ∠5 are also alternate interior angles.
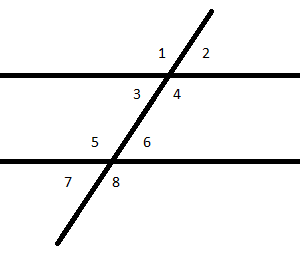
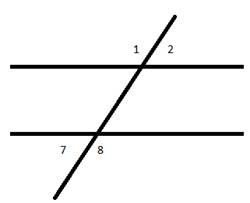
 Alternate Exterior Angles
Alternate Exterior Angles
Pairs of exterior angles on opposite sides of the transversal.
∠1 and ∠8 are alternate exterior angles.
∠ 2 and ∠7 are alternate exterior angles.
Corresponding angles
Pairs of angles in matching corners are called Corresponding Angles.
∠1 and ∠5 are corresponding angles.
∠2 and ∠6 are corresponding angles.
∠3 and ∠7 are corresponding angles
∠4 and ∠8 are corresponding angles.
 Try this:
Try this:
1. Write 1 pair of alternate exterior angle.
2. Write 1 pair of corresponding angle.
Answer:
1. ∠ a and ∠ h
2. ∠ b and ∠ f
Now try it yourself! Should you still need any help, click here to schedule live online session with e Tutor!
About eAge Tutoring:
eAgeTutor.com is the premium online tutoring provider. Using materials developed by highly qualified educators and leading content developers, a team of top-notch software experts, and a group of passionate educators, eAgeTutor works to ensure the success and satisfaction of all of its students.
Contact us today to learn more about our tutoring programs and discuss how we can help make the dreams of the student in your life come true!
Reference Links:
- http://en.wikipedia.org/wiki/Angle
- http://www.mathopenref.com/angleacute.html
- http://www.mathopenref.com/angleobtuse.html
- http://en.wikipedia.org/wiki/Right_angle
- http://www.mathopenref.com/anglestraight.html
- http://www.mathopenref.com/anglereflex.html
- http://en.wikipedia.org/wiki/Complementary_angles
- http://en.wikipedia.org/wiki/Supplementary_angles
- http://en.wikipedia.org/wiki/Adjacent_angle
- http://en.wikipedia.org/wiki/Vertical_angles
- http://www.khanacademy.org/video/angles-formed-between-transversals-and-parallel-lines?playlist=Geometry


 Alternate Exterior Angles
Alternate Exterior Angles