Introduction to Ellipses
An ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis. An ellipse is also the locus of all points of the plane whose distances to two fixed points add to the same constant.
Elements of a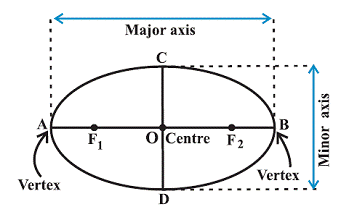 n Ellipse
n Ellipse
The two fixed points F1 and F2 are called the foci (plural of ‘focus’). The midpoint of the line segment joining the foci is called the centre of the ellipse. The line segment through the foci of the ellipse is called the major axis and the line segment through the centre and perpendicular to the major axis is called the minor axis. The end points of the major axis are called the vertices of the ellipse.
Suppose the lengths of the major axis and n=minor axis is 2a and 2b respectively. Also, the distance between the foci be 2c. Thus, the length of the semi major axis is ‘a’ and semi-minor axis is ‘b’.
Equations of an ellipse
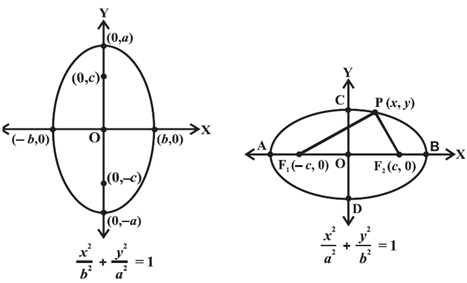
Above diagrams represent two possible orientations of ellipse.
Now, we will derive the equation for the ellipse with foci on the x – axis.
Let F1 and F2 be the foci and O be the midpoint of the line segment F1F2. Let O be the origin and the line from O through F2 be the
positive x-axis and that through F1 as the negative x-axis.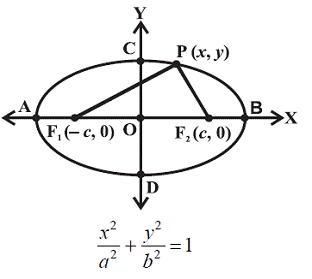
Let, the line through O perpendicular to the x-axis is the y-axis. Let the coordinates of F1 be (– c, 0) and F2 be (c, 0).
Let P(x, y) be any point on the ellipse such that the sum of the distances from P to the two foci be 2a so given
PF1 + PF2 = 2a
Applying distance formula in above equation:
√((x + c)2 + y2) + √((x – c)2 + y2)= 2a
√((x + c)2 + y2) = 2a - √((x – c)2 + y2)
Squaring both sides:
(x + c)2 + y2 = 4a2 – 4a√((x – c)2 + y2) + (x + c)2 + y2
On further simplification:
√((x - c)2 + y2) = a – cx/a
On further squaring and simplifying:
x2/a2 + y2/(a2 – c2) = 1
x2/a2 + y2/b2 = 1
Hence, any point on the ellipse satisfies:
x2/a2 + y2/b2 = 1
To summarise, here are the observations from the standard equations of ellipse:
1. Ellipse is symmetric with respect to both the coordinate axes since if (x, y) is a point on the ellipse, then (– x, y), (x, –y) and (– x, –y) are also points on the ellipse.
2. The foci always lie on the major axis. The major axis can be determined by finding the intercepts on the axes of symmetry. That is, major axis is along the x-axis if the coefficient of x2 has the larger denominator and it is along the y-axis if the coefficient of y2 has the larger denominator.
Eccentricity
The eccentricity for the ellipse x2/a2 + y2/b2 = 1,
We have:
b2 = a2 (1 – e2)
e2 = 1 – b2/a2
e2 = 1 - 4b2/4a2
e2 = 1 – (2b)2/(2a)2
e = √(1 – (Minor Axis/Major Axis)2)
Latus Rectum
Latus rectum of an ellipse is a line segment perpendicular to the major axis through any of the foci and whose end points lie on the ellipse.
The length of the latus rectum of ellipse x2/a2 + y2/b2 = 1 is 2b2/a.
Now try it yourself! Should you still need any help, click here to schedule live online session with e Tutor!
About eAge Tutoring:
eAgeTutor.com is the premium online tutoring provider. Using materials developed by highly qualified educators and leading content developers, a team of top-notch software experts, and a group of passionate educators, eAgeTutor works to ensure the success and satisfaction of all of its students.
Contact us today to learn more about our tutoring programs and discuss how we can help make the dreams of the student in your life come true!
Reference Links:
- http://en.wikipedia.org/wiki/Cone_(geometry)
- http://en.wikipedia.org/wiki/Circle
- http://en.wikipedia.org/wiki/Locus_(mathematics)
- http://en.wikipedia.org/wiki/Ellipse#Elements_of_an_ellipse
- http://en.wikipedia.org/wiki/Ellipse#Equations
- http://www.thefreedictionary.com/eccentricity
- http://www.answers.com/topic/latus-rectum