Definition
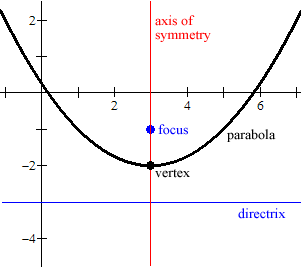 A parabola is the set of all points in a plane that are equidistant from a fixed line and a fixed point (not on the line) in the plane.
A parabola is the set of all points in a plane that are equidistant from a fixed line and a fixed point (not on the line) in the plane.
The fixed line is called Directrix of the parabola and the fixed point is called the Focus. A line through the focus and perpendicular to the Directrix is called the axis of the parabola. The point of intersection of parabola with the axis is called the Vertex of the parabola.
Equations of Parabola
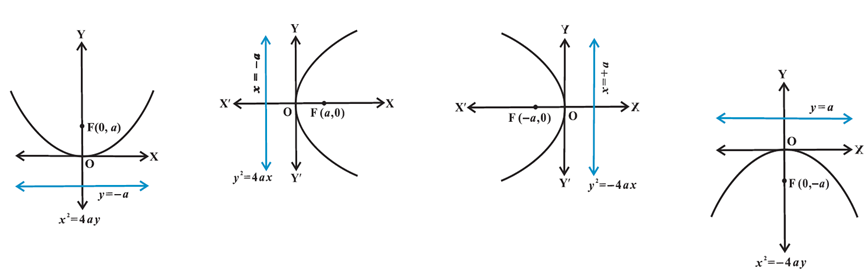
Above diagrams represent four possible orientations of parabola. Now, we will derive the equation for the parabola with focus at (a, 0) a> 0; and Directrix x = -a. Consider the following diagram:
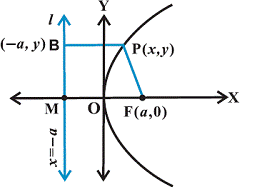 Let F be the focus and l the Directrix. Let FM be perpendicular to the Directrix and bisect FM at the point O. Extend MO to MX. Suppose the distance from the Directrix to the focus be 2a. Then, the coordinates of the focus are (a, 0) and the equation of Directrix is x + a = 0.
Let F be the focus and l the Directrix. Let FM be perpendicular to the Directrix and bisect FM at the point O. Extend MO to MX. Suppose the distance from the Directrix to the focus be 2a. Then, the coordinates of the focus are (a, 0) and the equation of Directrix is x + a = 0.
Let P (x, y) be any point on the parabola such that PF = PB, where PB is perpendicular to l. The coordinates of B are (-a, y).
Using distance formula, we have
PF = √((x – a) 2 + y2)
PB = √((x + a) 2)
Since, PF = PB
√((x – a) 2 + y2) = √((x + a) 2)
(x – a) 2 + y2 = (x + a) 2
x2 – 2ax + a2 + y2 = x2 + 2ax + a2
y2 = 4ax (a > 0)
Similarly, we can find other three equations of the parabola as shown in the above diagrams.
Thus, the four equations of parabola are:
Y2 = 4ax
Y2 = - 4ax
X2 = 4ay
X2 = - 4ay
These four equations are called the standard equations of parabola.
To summarise, here are the observations from the standard equations of parabola:
1. Parabola is symmetric with respect to the axis of the parabola.
If the equation is y2 = 4ax or -4ax, then the axis of symmetry is along the x-axis
And if the equation is x2 = 4ay or -4ay, then the axis of symmetry is along the y-axis.
2. When the axis of symmetry is along the x-axis the parabola opens to the
• Right - if the coefficient of x is positive.
• Left - if the coefficient of x is negative.
3. When the axis of symmetry is along the y-axis the parabola opens
• Upwards - if the coefficient of y is positive.
• Downwards - if the coefficient of y is negative.
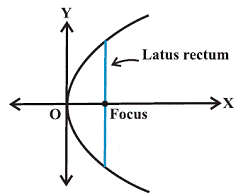
Latus Rectum
Latus rectum of a parabola is a line segment perpendicular to the axis of the parabola, through the focus and whose end points lie on the parabola.
To find the Length of the latus rectum: y2 = 4ax
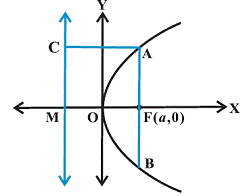 Consider the above diagram:
Consider the above diagram:
From the definition of the parabola, AF = AC.
But AC = FM = 2a
Hence AF = 2a.
And since the parabola is symmetric with respect to x-axis AF = FB and so
AB = Length of the latus rectum = 4a.
Now try it yourself! Should you still need any help, click here to schedule live online session with e Tutor!
About eAge Tutoring:
eAgeTutor.com is the premium online tutoring provider. Using materials developed by highly qualified educators and leading content developers, a team of top-notch software experts, and a group of passionate educators, eAgeTutor works to ensure the success and satisfaction of all of its students.
Contact us today to learn more about our tutoring programs and discuss how we can help make the dreams of the student in your life come true!
Reference Links:
- http://en.wikipedia.org/wiki/Parabola
- http://en.wikipedia.org/wiki/Directrix#Eccentricity.2C_focus_and_directrix
- http://en.wikipedia.org/wiki/Parabola#Equation_in_Cartesian_coordinates
- http://www.purplemath.com/modules/distform.htm
- http://www.thefreedictionary.com/Axis+of+symmetry
- http://www.answers.com/topic/latus-rectum