An equation involving trigonometric ratios of an angle is said to be a trigonometric identity if it is satisfied for all values of that angle for which the given trigonometric ratios are defined. Trigonometric identities are equalities that involve trigonometric functions and are true for every single value of the occurring variables.

We have three main trigonometric identities:
•    Sin² θ + Cos² θ = 1

•    Sec² θ = 1 + Tan² θ

•    Cot² θ + 1 = Cosec² θ

Let’s discuss each of the above trigonometric identity in detail:

Sin² θ + Cos² θ = 1

In the adjoining figure, we have Δ ABC right angled at C.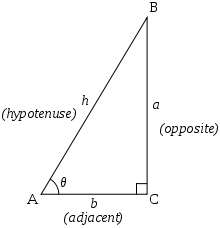

According to Pythagoras theorem:
AB² = AC² + BC² … (i)

Divide each term of above equation (i) by AB²

AB² = AC² + BC²    … (ii)
AB²     AB²     AB²

As we know, Sin θ = Opposite / Hypotenuse
Sin θ = BC / AB
And, Cos θ = Adjacent / Hypotenuse
Cos θ = AC / AB


Putting the values of Sin θ and Cos θ in equation (ii)
1 = Cos² θ + Sin² θ

This is true for all θ such that 0° ≤ θ ≤ 90°. So, this is a trigonometric identity.

Sec² θ = 1 + Tan² θ

In the adjoining figure, we have Δ ABC right angled at C.

According to Pythagoras theorem:
AB² = AC² + BC² … (i)

To prove next identity we will divide equation (i) by AC²

AB² = AC² + BC²    … (iii)
AC²     AC²    AC²

As we know, Secant θ = Hypotenuse / Adjacent
Secant θ = AB / AC
And, Tangent θ = Opposite / Adjacent
Tangent θ = BC / AC

Putting the values of Secant θ (Sec θ) and Tangent θ (Tan θ) in equation (iii)
Sec² θ = 1 + Tan² θ

Tan θ and Sec θ are not defined for θ = 90°

So the above equation is true for all θ such that 0° ≤ θ < 90°

Cot² θ + 1 = Cosec² θ

In the adjoining figure, we have Δ ABC right angled at C.

According to Pythagoras theorem:
AB² = AC² + BC² … (i)

Next we will divide equation (i) by BC²

AB² = AC² + BC²    … (iv)
BC²     BC²     BC²

As we know, Cotangent θ = Adjacent / Opposite
Cotangent θ = AC / BC
And, Cosecant θ = Hypotenuse / Opposite
Cosecant θ = AB / BC


Putting the values of Cosecant θ (Cosec θ) and Cotangent θ (Cot θ) in equation (iv)
Cosec² θ = Cot² θ + 1
Cot θ and Cosec θ are not defined for θ = 0°

So the above equation is true for all θ such that 0° < θ ≤ 90°

Using these identities, we can convert each trigonometric ratio in terms of other trigonometric ratios, that is, if any one of the ratios is known, we can also find the values of other trigonometric ratios.

Now try it yourself!  Should you still need any help, click here to schedule live online session with e Tutor!

About eAge Tutoring:

eAgeTutor.com is the premium online tutoring provider.  Using materials developed by highly qualified educators and leading content developers, a team of top-notch software experts, and a group of passionate educators, eAgeTutor works to ensure the success and satisfaction of all of its students.

Contact us today to learn more about our tutoring programs and discuss how we can help make the dreams of the student in your life come true!

Reference Links:

•     http://www.purplemath.com/modules/basirati.htm
•     http://en.wikipedia.org/wiki/List_of_trigonometric_identities
•     http://en.wikipedia.org/wiki/Pythagorean_theorem
•     http://en.wikipedia.org/wiki/Sine
•     http://en.wikipedia.org/wiki/Trigonometric_functions#Sine.2C_cosine.2C_and_tangent