Introduction to Bounded Regions
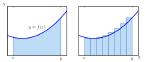 In this article we will study a specific application of integrals to find the area under simple curves, area between lines and arcs of circles, parabolas and ellipses.
In this article we will study a specific application of integrals to find the area under simple curves, area between lines and arcs of circles, parabolas and ellipses.
Area under simple curves
The area bounded by the curve y = f(x), x-axis and the ordinates x = a and x = b is given by A= a∫b y dx= a∫b f(x) dx
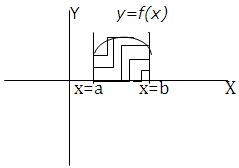
The area A of the region bounded by the curve x = g(y), y-axis and the lines y = c and y = d is given by
A = c∫d x dy = c∫d g(y) dy
Example: Find the area of the region bounded by the curve y2 = 9x, x = 2, x = 4 and the x-axis in the first quadrant.
Solution: Area = 2∫4 y dx
= 2∫4 3√x dx
= 3 [x3/2 / (3/2)]24
= (16 - 4√2) sq. units
Area between a curve and a line
Example: Find the area of the smaller part of the circle x2 + y2 = a2 cut off by the line x = a/√2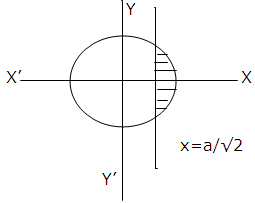
Solution: x2 + y2 = a2 ………….(1)
x = a/√2 …………..(2)
Solving (1) and (2) we will get the point of intersection
We have to find the area of shaded region which is given by
A=2*[ a/√2∫a Area under the curve (y2 = a2 - x2) dx]
= 2 a/√2∫a√(a2 - x2) dx
= 2 [x/2 (√a2 - x2) – (a2/2) sin-1 (x/a)]a/√2a
= a2/2 [(π/2) – 1] sq. units
Area between two curves
 Example: Find the area lying above x-axis and included between the circle x2 + y2 = 8x and inside the parabola y2 = 4x
Example: Find the area lying above x-axis and included between the circle x2 + y2 = 8x and inside the parabola y2 = 4x
Solution: The given equation of the circle x2 + y2 = 8x can be expressed as (x - 4)2 + y2 = 16, which is a circle with center (4, 0) and radius 4.
The point of intersection gives x = 0, 4
Hence the curves intersect at O (0, 0) and P (4, 4) above the x-axis.
Required area=2 0∫4 √x dx+ 4∫8 √(42 - (x - 4)2) dx
=2(2/3) [x3/2]04 + [((x-4)/2) √(42-(x-2)2) + (42/2)sin-1(x-2)/2]48
= 32/3 + [4/2 *0+1/2 *16*sin-1(1)]
= (32/3) + 4π
= (4/3) (8 + 3π) sq. units
Now try it yourself! Should you still need any help, click here to schedule live online session with e Tutor!
About eAge Tutoring:
eAgeTutor.com is the premium online tutoring provider. Using materials developed by highly qualified educators and leading content developers, a team of top-notch software experts, and a group of passionate educators, eAgeTutor works to ensure the success and satisfaction of all of its students.
Contact us today to learn more about our tutoring programs and discuss how we can help make the dreams of the student in your life come true!