Introduction to Average Values
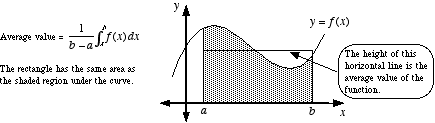 If ‘f’ is continuous on [a, b], then the average value (mean value) of ‘f’ on [a, b] is defined to be
If ‘f’ is continuous on [a, b], then the average value (mean value) of ‘f’ on [a, b] is defined to be
fave = 1 ∫ab f(x)dx
b-a
Proof: Arithmetic mean or average is formed by adding the data and dividing by the number of data points. Thus, the arithmetic average a of n numbers a1, a2, …….., an is
![]()
In the case where the ak’s are values of a function f, say.
a1=f(x1), a2=f(x2)… an = f(xn), then the arithmetic average a of these function values is
![]()
Now we can see how to extend this concept so that we can compute not only the arithmetic average of finitely many function values but an average of all values of f(x) as x varies over a closed interval [a, b]. For this purpose recall the Mean-Value Theorem for Integrals, which states that if f is continuous on the interval [a, b], then there is at least one number x* in this interval such that
∫abf(x)dx = f(x*)(b-a)
f(x*) = 1 ∫ab f(x)dx
b-a
This will be the average value of ‘f’ over the interval [a, b]. Divide the interval [a, b] into n sub intervals of equal length
∆x = b-a
n
Choose arbitrary numbers x1*, x2*, …………, xn* in successive sub-intervals. Then the arithmetic average of the values f(x1*), f(x2*) ……..f(xn*) is
![]()
From (1), ave = 1 [f(x1*)∆x+f(x2*)∆x+……….+f(xn*)∆x]
b-a
Taking the limit as n— +∞ yields
lim 1Σf(xk*)∆x = 1 ∫ab f(x)dx
n— +∞ b-a b-a
Since this equation describes what happens when we compute the average of “more and more” values of f(x), we get the result,
fave = 1 ∫abf(x)dx
b-a
Example: Find the average value of the function f(x)=√x over the interval [1, 4]
Solution: fave = 1 ∫ab f(x)dx
b-a
= 1 ∫14 √xdx
4-1
![]()
9
= 14/9
≈ 1.6
Mean Value Theorem for Integrals
If ‘f’ is continuous on a closed interval [a, b] then there is at least one number x* in [a, b] such thata∫b f(x)dx = f(x*)(b-a)
Proof: By the Extreme-Value Theorem, f assumes a maximum value M and a minimum value m on [a, b]. Thus for all x in [a, b]
a∫b mdx ≤ a∫b f(x)dx ≤ a∫b Mdx
m(b-a) ≤ a∫b f(x)dx ≤M(b-a)
m ≤1 a∫b f(x) ≤M
b – a
This implies that 1/(b-a) a∫bf(x)dx is a number between m and M and since f(x) assumes the values m and M on [a, b] if follows from the Intermediate Value Theorem that f(x) must assume the value 1/(b-a)a∫b f(x)dx at some x* in [a, b]; that is,
1/(b-a) a∫b f(x)dx = f(x*)
a∫bf(x)dx = f(x*)(b-a)
Fundamental Theorem of Calculus
If ‘f’ is continuous on an interval I, then ‘f’ has an anti derivative on I. In particular, if a is any number in I, then the function F defined by
F(x) = a∫x f(t)dt
Is an anti derivative of f on I; that is F’(x) =f(x) for each x in I, or in an alternative notation.
d [a∫x f(t)dt] = f(x)
dx
Example: Find d/dx [1∫xt3dt] by applying second part of Fundamental Theorem of Calculus and then confirm the result by performing the integration and then differentiating.
Solution: The integrand is continuous function so
d [ 1∫xt3dt] = x3
dx
Evaluating the integral and then differentiating yields
![]()
![]()
Hence the two methods for differentiating the integral agree.
Two methods for making substitutions in definite integrals
Indefinite integrals of the form ∫f[g(x)]g’(x)dx can sometimes be evaluated by making the u-substitution
Take u= g(x), du=g’(x) dx which converts the integral to the form ∫f(u)du
To apply this method to a definite integral of the form a∫bf[g(x)]g’(x)dx we need to account for the effect that the substitution has on the x-limits of integration. There are two ways of doing this.
Method 1: First evaluate the indefinite integral ∫f[g(x)]g’(x)dx by substitution and then the relationship a∫bf[g(x)]g’(x)dx = [∫f[g(x)]g’(x)dx]ab to evaluate the definite integral. This procedure does not require any modification of x-limits of integration.
Method 2: Make the substitution given above directly in the definite integral, and then use the relationship u=g(x) to replace the x-limits, x=a and x=b by corresponding u-limits, u=g(a) and u=g(b). This produces a new definite integral
g(a)∫g(b) f(u)du that is expressed entirely in terms of u.
Example: Use the two methods to evaluate 0∫2x(x2+1)3dx
Solution:
First Method: u=x2+1, du = 2xdx
∫x(x2+1)3dx = ½ ∫u3du = u4/8 +c = (x2+1)4/8 +C
0∫2x(x2+1)3dx = [(x2+1)/8]02
= 625/8 – 1/8
= 78
Second Method: Put u=x2+1 du=2xdx
When x=0, u=0+1 =1
x=2, u=4+1 = 5
0∫2x(x2+1)3dx = ½ 1∫5u3du = [u4/8]15
= 625/8 – 1/8
= 78
Now try it yourself! Should you still need any help, click here to schedule live online session with e Tutor!
About eAge Tutoring:
eAgeTutor.com is the premium online tutoring provider. Using materials developed by highly qualified educators and leading content developers, a team of top-notch software experts, and a group of passionate educators, eAgeTutor works to ensure the success and satisfaction of all of its students.
Contact us today to learn more about our tutoring programs and discuss how we can help make the dreams of the student in your life come true!