Introduction
Here we are dealing with a test that is useful in its own right and is also the building block for other important convergence tests. The underlying idea of this test is to use the known convergence or divergence of a series to deduce the convergence or divergence of another series.Theorem: Let Σak and Σbk be series with non-negative terms and suppose that a1 ≤ b1, a2 ≤ b2, a3 ≤ b3 ………ak ≤ bk, …………….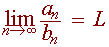 a) If the “bigger series” Σbk converges, then the “smaller series” Σak also converges.
a) If the “bigger series” Σbk converges, then the “smaller series” Σak also converges.
b) If the “smaller series” Σak diverges, then the “bigger series” Σbk also diverges.
Using the Comparison Test
There are two steps required for using the comparison test to determine whether a series Σuk with positive terms converges:
Step I: Guess at whether the series Σuk converges or diverges.
Step II: Find a series that proves the guess to be correct. That is, if the guess is divergence, we must find a divergent series whose terms are “smaller” than the corresponding terms of Σuk, and if the guess is convergence, we must find a convergent series whose terms are “bigger” than the corresponding terms of Σuk.
In most cases, the series Σuk being considered will have its general term uk expressed as a fraction. To help with the guessing process in the first step, we have formulated two principles that are based on the form of the denominator for uk. These principles are called informal principles because they are not intended as formal theorems.
Informal Principle 1: Constant summands in the denominator of uk can be usually be deleted without affecting the convergence or divergence of the series.
Informal Principle 2: If a polynomial in ‘k’ appears as a factor in the numerator or denominator of uk, all but the leading term in the polynomial can usually be discarded without affecting the convergence or divergence of the series.
Problems related to comparison test
Use the comparison test to determine whether the following series converge or diverge.
1. Σ 1 2. Σ 1
√k – ½ 2k2 + k
1. According to principle 1, we should be able to drop the constant in the denominator without affecting the convergence or divergence. Thus, the given series is likely to behave like Σ 1/√k which is a divergent p-series (p=1/2). Thus, we will guess that the given series diverges and try to prove this by finding a divergent series that is “smaller” than the given series.
1 > 1 for k=1, 2, ………
√k – ½ √k
Thus, we have proved that the given series diverges.
2. According to Principle 2, we should be able to discard all but the leading term in the polynomial without affecting the convergence or divergence. Thus, the given series is likely to behave like
Σ (1/2k2) = ½ Σ(1/k2) which converges since it is a constant times a convergent p-series (p=2). Thus, we will guess that the given series converges and try to prove this by finding a convergent series that is “bigger” than the given series.
1 < 1 for k=1, 2, 3…….
2k2 + k 2k2
Thus, we have proved that the given series converges.
Limit Comparison Test
In the previous two problems the informal principles provided the guess about convergence or divergence as well as the series needed to apply the comparison test. It is not always easy enough to find the series required for comparison, so we will now consider an alternative to the comparison test that is usually easier to apply.
Let Σak and Σbk be series with positive terms and suppose that
![]()
If ρ is finite and ρ > 0, then the series both converge or both diverge.
Problems related to limit comparison test
Use the limit comparison test to determine whether the following series converge or diverge
1. Σ 1
√k – 1
2. ![]()
1. To prove that the given series diverges, we will apply the limit comparison test with ak = 1/[√k – 1] and bk = 1/√k
We obtain, ![]()
Since ρ is finite and positive, it follows that the given series diverges.
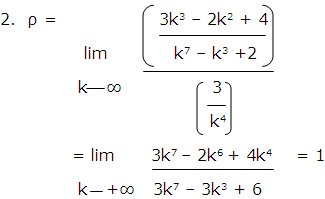
Since ρ is finite and nonzero, it follows that the given series converges.
Now try it yourself! Should you still need any help, click here to schedule live online session with e Tutor!
About eAge Tutoring:
eAgeTutor.com is the premium online tutoring provider. Using materials developed by highly qualified educators and leading content developers, a team of top-notch software experts, and a group of passionate educators, eAgeTutor works to ensure the success and satisfaction of all of its students.
Contact us today to learn more about our tutoring programs and discuss how we can help make the dreams of the student in your life come true!