Differentiation of Vectors

If a vector R varies continuously as a scalar variable t changes, then R is said to be a function of t and is written as R = F(t).
Just as in scalar calculus, we define derivative of a vector function R = F(t) as
![]() and write it as dR/dt or dF/dt or F'(t).
and write it as dR/dt or dF/dt or F'(t).
General rules of differentiation are similar to those of ordinary calculus provided the order of factors in vector products is maintained. Thus, if Ф, F, G, H are scalar and vector functions of a scalar variable t, we have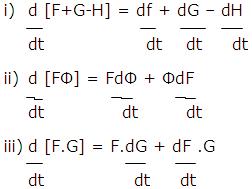
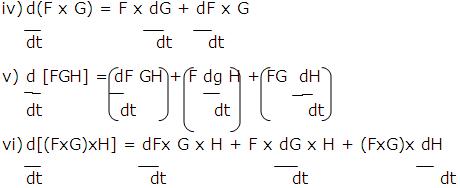

Example: If A= 5t2I + tJ – t3K, B=sintI - cos(t)J then
Find i) d/dt(A.B)
ii) d/dt(AxB)
Solution: i) d/dt(A.B) = A.(dB/dt) + (dA/dt).B
= (5t2I+tJ-t3K)[costI –(-sint)J] + (10tI+J-3t2K)(sintI - costJ)
= (5t2cost-tsint) + (10tsint-cost)
= 5t2 cos(t) + 11tsin(t) – cos(t).
ii) d/dt(AXB) = Ax(dB/dt) + (dA/dt)xB
= (5t2I+tJ-t3K)x(costI +sintJ) + (10tI+J-3t2K)x(sintI -costJ)
= (t3sint-3t2cost)I – t2(tcost+3sint)J + [(5t2-1)sint-11tcost]K
Derivative of Polar Functions
Let r = r(θ) represent a polar curve, then
dy = dy/dθ = r'sinθ + rcosθ
__ ______ ______ _____
dx dx/dθ r'cosθ – rsinθ
Since x=rcosθ
dx/dθ = r(-sinθ) + cosθ. r' = r'cosθ – rsinθ
y = rsinθ
dy/dθ = rcosθ + sinθ. r' = r'sinθ + rcosθ
dy = dy/dθ = r'sinθ + rcosθ
___ ______ ______ ______
dx dx/dθ r'cosθ – rsinθ
Example: Find the derivative of r = θcosθ
Example: dy/dx = [θ(-sinθ) + cosθ] sinθ + θ cosθ (cosθ)
________________________________
[θ(-sinθ) + cosθ] cosθ – θ cosθ sinθ
= -θsin2θ + cosθ sinθ + θcos2θ
_________________________
-θsinθ cosθ + cos2θ – θcosθ sinθ
= cosθ sinθ + θ(cos2θ – sin2θ)
_________________________
cos2θ - 2θ cosθ sinθ
= cosθ sinθ+ θcos2θ
_______________
cos2θ - 2θ cosθ sinθ
Example: Find the slope of the tangent line to the unit circle x= cost, y = sint (0≤t≤2π) at the point t = π/6
Solution: The slope at a general point on the circle is dy/dx![]()
Thus, the slope at t = π/6 is
dy/dx]t=π/6 = -cot π/6 = -√3
Example: Find the slope of the tangent line to the circle r = 4cosθ at the point where θ = π/4
Solution: ![]()
Thus, at the point where θ = π/4 the slope of the tangent line is dy/dx]θ=π/4 = -cotπ/2 = 0 which implies that the circle has a horizontal tangent line at the point where θ = π/4
Now try it yourself! Should you still need any help, click here to schedule live online session with e Tutor!
About eAge Tutoring:
eAgeTutor.com is the premium online tutoring provider. Using materials developed by highly qualified educators and leading content developers, a team of top-notch software experts, and a group of passionate educators, eAgeTutor works to ensure the success and satisfaction of all of its students.
Contact us today to learn more about our tutoring programs and discuss how we can help make the dreams of the student in your life come true!