Introduction
In this topic, we are dealing with different types of differentiation. Different methods are derivatives of implicit functions, exponential functions, and logarithmic functions.
Derivatives of Implicit Functions
When a relationship between x and y is expressed in a way that it is easy to solve for y and write y=f(x), we say that y is given as an explicit function of 'x', otherwise it is implicit that y is a function of x and we say that the relationship gives function implicitly.
For example: 1) 2x+3y+5=0
2) x+cosxy+3=0
In the above examples, first one is an explicit function, since it can be easily written as y= (-2x-5)/3 and is easy to solve for y.
But in the second one, we find difficult to separate y from that function, so it is an implicit function. In the case of an implicit function, we directly differentiate the given function with respect to x and find dy/dx.
Find dy/dx for the function ax + by2 = Cos y
Differentiating with respect to x we get,
a. 1+b. 2ydy/dx= -siny dy/dx
(2by+siny)dy/dx = -a
![]()
Exponential Function
The exponential function with positive base b>1 is the function y=bx
The domain of the exponential function is R, the set of real numbers and the range is set of all positive real numbers.
Exponential function with base 10 is called the common exponential function, which is given by y=10x
Using 'e' as the base, we get an extremely important exponential function y=ex which is called natural exponential function
The derivative of ex is ex itself
![]()
The derivative of bx is given by, ![]()
Logarithmic Function
Let b>1 and if bx=a, then we say logarithm of 'a' to the base 'b' is 'x' and it is denoted by logba=x. This function is defined from R+ to R.
The domain of logarithmic function is R+ and the range is R, set of all real numbers.
If the base b=10, then we say it as common logarithm and if b=e then it is natural logarithm.
The derivative of log function is given by
![]()
Logarithmic Differentiation
Logarithmic differentiation is applicable for the functions in the form
y= [u(x)]v(x), taking log on both sides we get,
log y = log[u(x)]v(x)
= v(x) log[u(x)]
Using Chain Rule, we may differentiate this to get,
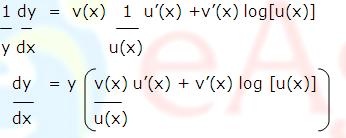
The main point to be noted in this method is that 'y' and u(x) must always be positive otherwise their logarithms are not defined. This process of differentiation is known as Logarithmic Differentiation.
Laws of logarithms
1) logb pq= logbp + logbq
2) logb(p/q)= logbp – logbq
3) logbpq = qlogbp [Power Rule]
4) loga p = logbp [ Change of Base]
_____
logba
Example: Differentiate xsinx, x>0 w.r.t x
Solution: Let y = xsinx
Taking log on both sides,
log y = log xsinx
log y = sinx logx
Differentiating,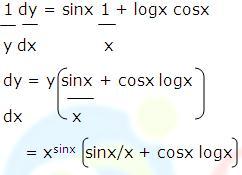
Now try it yourself! Should you still need any help, click here to schedule live online session with e Tutor!
About eAge Tutoring :
eAgeTutor.com is the premium online tutoring provider. Using materials developed by highly qualified educators and leading content developers, a team of top-notch software experts, and a group of passionate educators, eAgeTutor works to ensure the success and satisfaction of all of its students.
Contact us today to learn more about our tutoring programs and discuss how we can help make the dreams of the student in your life come true!
Reference Links :
- http://en.wikipedia.org/wiki/Implicit_and_explicit_functions
- http://en.wikipedia.org/wiki/Logarithmic_differentiation
- http://en.wikipedia.org/wiki/Exponential_function
- http://www.intmath.com/functions-and-graphs/2a-domain-and-range.php
- http://en.wikipedia.org/wiki/Logarithm
- http://en.wikipedia.org/wiki/Derivative