Introduction
 Here we will discuss about motion of particles along a line. The motion of particles along a line is called rectilinear motion. In general rectilinear motion, a particle can move back and forth along the line (as with a piston moving up and down in a cylinder).However, we will consider the simple case in which the particle moves in just one direction along a line (as the car traveling on a straight road). We will assume the motion along a coordinate line, such as an x-axis or y-axis, and that the particle is moving in the positive direction.
Here we will discuss about motion of particles along a line. The motion of particles along a line is called rectilinear motion. In general rectilinear motion, a particle can move back and forth along the line (as with a piston moving up and down in a cylinder).However, we will consider the simple case in which the particle moves in just one direction along a line (as the car traveling on a straight road). We will assume the motion along a coordinate line, such as an x-axis or y-axis, and that the particle is moving in the positive direction.
For a particle in rectilinear motion along a coordinate axis, the average velocity of the particle during the time interval from t0 to t1 is given by
vave = s1 – s0 = ∆s
________ ___
t1 – t0 ∆t
where s0 and s1are the coordinates of the particle at times t0 and t1 respectively.
Hence the average velocity over a time interval is the displacement during the time interval divided by the length of the time interval. In special case where the average velocity of a particle in rectilinear motion is the same over every time interval, the particle is said to have constant velocity or uniform rectilinear motion.
If s(t) is the position function of a particle moving on a coordinate line, then the instantaneous velocity of the particle at time 't' is defined by
v(t) = s'(t) = ds/dt
Since the instantaneous velocity at a given time is equal to the slope of the position versus time curve at that time, the sign of the velocity tells us which way the particle is moving- a positive velocity means that s is increasing with time, so the particle is moving in the positive direction; a negative velocity means that s is decreasing with time, so the particle is moving in the negative direction.
If s(t) is increasing then s'(t)>0 and if s(t) is decreasing then s'(t)<0.
Speed versus velocity
Speed describes how fast an object is moving without regard to direction, whereas velocity describes how fast it is moving and in what direction. Instantaneous speed of a particle is the absolute value of its instantaneous velocity
Instantaneous speed at time t = |v(t)| = |ds/dt|
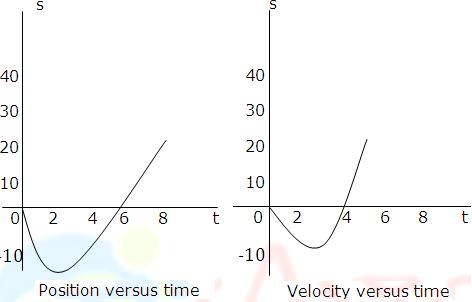
Example: Let s(t) = t3 - 6t2 be the position function of a particle moving along an s-axis, where s is in meters and t is in seconds. Find the instantaneous velocity and speed and show the graphs of position, velocity and speed versus time.
Solution: Instantaneous velocity, v(t) = ds/dt
= 3t2 – 12t
Instantaneous speed, |v(t)| = |3t2-12t|
The graphs of position, velocity and speed versus time are shown below. Velocity and speed both have units of m/s, since s is in meters and time in seconds.

Acceleration
In rectilinear motion, the rate at which the velocity of a particle changes with time is called its acceleration.
If s(t) is the position function of a particle moving on a coordinate line, then the instantaneous acceleration of the particle at time t is defined by
a(t) = v'(t) = dv/dt
Or
a(t) = s"(t) = d2s/dt2
Example: Let s(t)=t3-6t2 be the position function of a particle moving along an s-axis, where s is in meters and t is in seconds. Find the instantaneous acceleration a(t) and show the graph of acceleration versus time.
Solution: Given s(t) = t3-6t2
v(t) = ds/dt = 3t2-12t
a(t) = d2s/dt2 = 6t-12
The acceleration versus time curve is a line as shown in the figure and its unit is m/s2, since v is in meters per second and time is in seconds.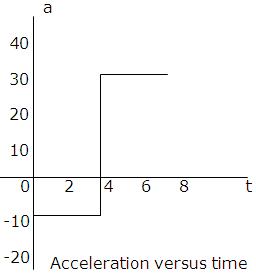
Speeding up and slowing down
A particle in rectilinear motion is speeding up when its instantaneous speed is increasing and is slowing down when its instantaneous speed is decreasing. Speeding up is called accelerating and slowing down is called decelerating.
A particle in rectilinear motion is speeding up when its velocity and acceleration have the same sign and slowing down when they have opposite signs.
Analyzing position versus time curve
The position versus time curve contains all of the significant information about the position and velocity of a particle in rectilinear motion:
- If s(t)>0, the particle is on the positive side of the s-axis.
- If s(t)<0, the particle is on the negative side of the s-axis.
- The slope of the curve at any time is equal to the instantaneous velocity at that time.
- Where the curve has positive slope, the velocity is positive and the particle is moving in the positive direction.
- Where the curve has negative slope, the velocity is negative and the particle is moving in the negative direction.
- Where the slope of the curve is zero, the velocity is zero, and the particle is momentarily stopped.
Now try it yourself! Should you still need any help, click here to schedule live online session with e Tutor!
About eAge Tutoring:
eAgeTutor.com is the premium online tutoring provider. Using materials developed by highly qualified educators and leading content developers, a team of top-notch software experts, and a group of passionate educators, eAgeTutor works to ensure the success and satisfaction of all of its students.
Contact us today to learn more about our tutoring programs and discuss how we can help make the dreams of the student in your life come true!