Introduction

The statements of Fundamental theorem of Calculus are as followed:
a) If ‘f’ is continuous on an interval I, then f has an anti derivative on I. In particular, if a is any number in I, then the function F defined by
F(x) = a∫x f(t)dt is an anti derivative of f on I; that is, F’(x) = f(x) for each x in I, or in an alternative notation ![]()
b) Let f be continuous function defined on the [a, b] and F be an anti-derivative of f, then
a∫b f(x) dx = [F(x)]ab
= F(b) – F(a)
Explanation
We will show first that F(x) is defined at each x in the interval I. If x>a and x is in the interval I, then by the theorem if a function f is continuous on an interval [a, b], then f is integrable on [a, b] can be applied to the interval [a, x] and the continuity of f on I ensure that F(x) is defined; and if x is in the interval I and x≤a, then the above theorem ensures that F(x) is defined. Thus, F(x) is defined for all x in I.
Next we will show that F’(x) = f(x) for each x in the interval I. If x is not an endpoint of I, then it follows from the definition of a derivative that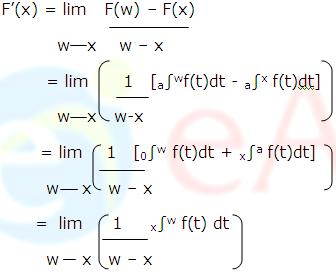
Applying the Mean Value Theorem for Integrals of x∫w f(t)dt, we obtain![]()
Where t* is some number between x and w. Because t* is between x and w, it follows that t* x as w x. Thus f(t*) f(x) as w x, since f is assumed continuous at x. Therefore, it follows from the above two equations that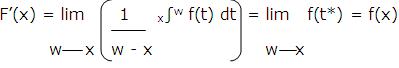
If x is an endpoint of the interval I, then the two sided limits in the proof must be replaced by the appropriate one sided limits, but otherwise the arguments are identical.
In other words, the formula states that
If a definite integral has a variable upper limit of integration, a constant lower limit of integration, and a continuous integrand, then the derivative of the integral with respect to its upper limit is equal to the integrand evaluated at the upper limit.
Problems based on Fundamental Theorem of Calculus

So the two methods for differentiating the integral agree.
2) Evaluate 2∫3 x2 dx
Solution: ∫x2 dx = x3/3=F(x) so therefore by the second fundamental theorem we get
I=F [3]-F [2]
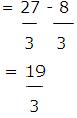
3) Evaluate 2∫3 (1/x)dx
Solution: We have ∫(1/x)dx = log|x| + C
So, 2∫3 (1/x)dx = [log|x|]23
= log 3 – log 2
=log 3/2
Differentiation and Integration are Inverse Processes
The two parts of the Fundamental Theorem of Calculus, when taken together, tell us that differentiation and integration are inverse processes in the sense that each undoes the effect of the other.
a∫x f’(t)dt = f(x) – f(a) which tells us that if the value of f(a) is known, then the function f can be recovered from its derivative f’ by integrating. Conversely part 2 of the Fundamental Theorem of Calculus states that
d/dx [a∫xf(t)dt] = f(x) which tells us that the function f can be recovered from its integral by differentiating. Thus, differentiation and integration can be viewed as inverse processes.
Now try it yourself! Should you still need any help, click here to schedule live online session with e Tutor!
About eAge Tutoring:
eAgeTutor.com is the premium online tutoring provider. Using materials developed by highly qualified educators and leading content developers, a team of top-notch software experts, and a group of passionate educators, eAgeTutor works to ensure the success and satisfaction of all of its students.
Contact us today to learn more about our tutoring programs and discuss how we can help make the dreams of the student in your life come true!
Reference Links:
http://en.wikipedia.org/wiki/Fundamental_theorem_of_calculushttp://en.wikipedia.org/wiki/Differentiation
http://en.wikipedia.org/wiki/Mean_value_theorem
http://en.wikipedia.org/wiki/Continuous_function