Introduction
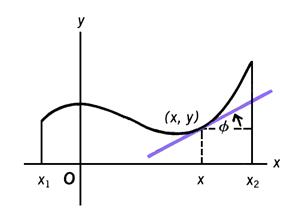
The main idea of derivative is that of rate of change of a function. The primary mathematical tool that is used to calculate rate of change and the slopes of curves is derivative. Slope of the graph of y=f(x) at x=x0is given by ![]()
The ratio ![]() is called a difference quotient.
is called a difference quotient.
The difference quotient can also be interpreted as the average rate of change of f(x) over the interval [x0, x1] and its limit as x1 x0 is the instantaneous rate of change of f(x) at x=x0.
Derivative of a function
Suppose that x0 is a number in the domain of a function f then the derivative of ‘f’ at x=x0 and is denoted by f’(x0) and is defined as
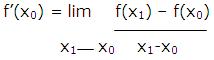
If the limit of the difference quotient exists, f’(x0) is the slope of the graph of ‘f’ at the point x=x0. If this limit does not exist, then the slope of the graph of ‘f’ is undefined at x=x0
Example: Find the slope of the function y=x2+1 at the point (2, 5)
Solution: Slope of the curve at the point (2, 5) is given by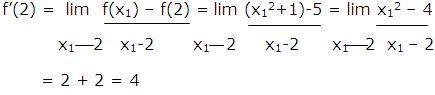
Graphical representation of Derivative
Suppose that x0 is a number in the domain of a function ‘f’. If![]()
then we define the tangent line to the graph of f at the point P(x0, f(x0) to be the line whose equation is y – f(x0) = f’(x0)(x-x0).
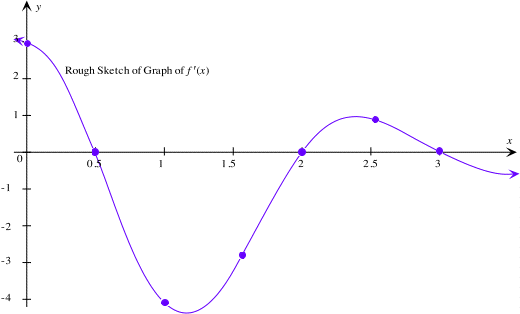
Below is the graph of a function f(x) and a rough sketch of f’(x). The graph of f’(x) represents the slopes of the tangent lines to a point on the graph for each x-value in the domain of f(x). For example if one draws a tangent line through the point (0.5, 3) its slope will be zero. Looking at the graph of f’(x) at x=0.5, y=0
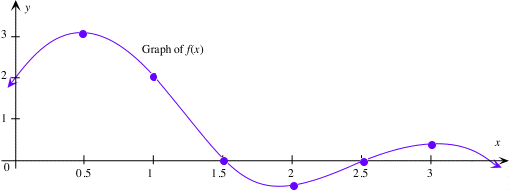
Example: Find the derivative with respect to x of f(x)=x3-x. Graph f and f’ together and discuss the relationship between the two graphs
Solution:
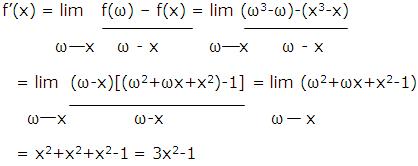
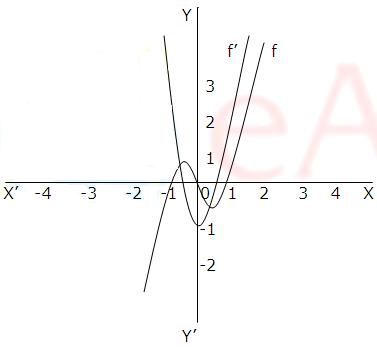
Since f’(x) can be interpreted as the slope of the graph of y=f(x) at x, the derivative f’(x) is positive where the graph of f has positive slope, it is negative where the graph of f has negative slope, and it is zero where the graph of f is horizontal.
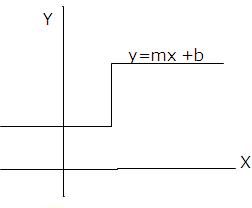
Interpretation of the derivative
The derivative f’ of a function f can be interpreted as a function whose value at x is the slope of the graph of y=f(x) at x, or alternatively, it can be interpreted as a function whose value at x is the instantaneous rate of change of y with respect to x at x. In particular, when y=f(t) describes the position at time t of an object moving along a straight line, then f’(t) describes the position at time t of an object moving along a straight line, then f’(t) describes the instantaneous velocity of the object at time ‘t’.
From the figure at each value of ‘x’, the tangent line to a line y=mx+b coincides with the line itself and hence all tangent lines have slope m. This suggests geometrically that if f(x) = mx + b, then f’(x) = m for all x. This is confirmed by the following computations:
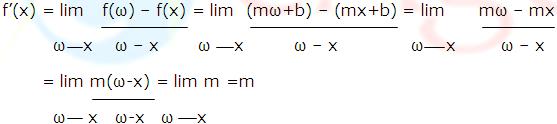
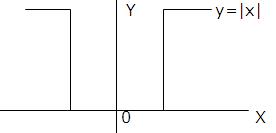
Example: The graph of y=|x| has a corner at x=0 which implies that f(x)=|x| is not differentiable at x=0
a) Prove that f(x)=|x| is not differentiable at x=0 by showing that the limit does not exist at x=0
b) Find a formula for f’(x)
Solution: From the definition
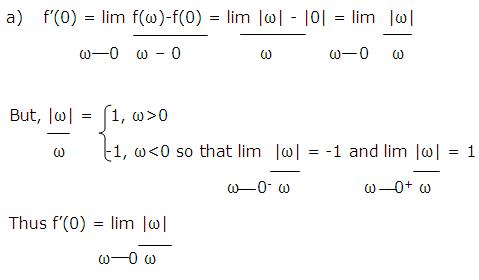
does not exist because the one sided limits are not equal.
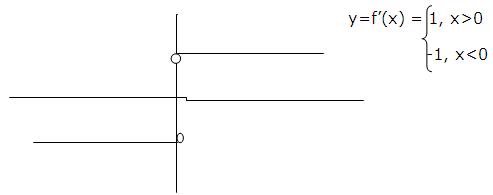
b) A formula for the derivatives of f(x) =|x| can be obtained by writing |x| in piecewise form and treating the cases x>0 and x<0 separately. If x>0, then f(x) =x and f’(x)=1; if x<0, then f(x)-x and f’(x)=-1. Thus,
![]()
The graph of f’ is shown below. We can see that f’ is not continuous at x=0. This shows that a function that is continuous everywhere may have a derivative that fails to be continuous everywhere
Now try it yourself! Should you still need any help, click here to schedule live online session with e Tutor!
About eAge Tutoring:
eAgeTutor.com is the premium online tutoring provider. Using materials developed by highly qualified educators and leading content developers, a team of top-notch software experts, and a group of passionate educators, eAgeTutor works to ensure the success and satisfaction of all of its students.
Contact us today to learn more about our tutoring programs and discuss how we can help make the dreams of the student in your life come true!
Reference Links:
- http://en.wikipedia.org/wiki/Derivative
- http://en.wikipedia.org/wiki/Difference_quotient
- http://en.wikipedia.org/wiki/Slope
- http://en.wikipedia.org/wiki/Tangent_lines_to_circles