Introduction
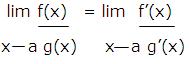 The limit lim [f(x)/g(x)] is, in general, equal, to the limit of the numerator x a divided by the limit of the denominator. But when lim f(x) and lim g(x) are both zero, the quotient takes the form 0/0 which is meaningless.
The limit lim [f(x)/g(x)] is, in general, equal, to the limit of the numerator x a divided by the limit of the denominator. But when lim f(x) and lim g(x) are both zero, the quotient takes the form 0/0 which is meaningless.
But lim [f(x)/g(x)] may not be meaningless, which mean that it may exist. In this article, we shall consider how to obtain the limiting values in such and similar other cases.
L’Hospital’s Rule for the form 0/0: Suppose that f and g are differentiable functions on an open interval containing x=a, except possibly at x=a, and that
![]()
If lim[f’(x)/g’(x)] has a finite limit or if this limit is +∞ or -∞, then x a
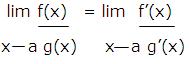
Moreover, this statement is also true in the case of a limit as x -a-, x - a+, x - -∞ or as x- +∞
Note that in L’Hospital’s rule the numerator and denominator are differentiated separately, which is not the same as differentiating f(x)/g(x).
The following steps are used while solving problems:
Step I: Check that the limit of f(x)/g(x) is an indeterminate form. If it is not, then L’Hospital’s rule cannot be used.
Step II: Differentiate f and g separately.
Step III: Find the limit of f’(x)/g’(x). If this limit is finite, +∞, or -∞, then it is equal to the limit of f(x)/g(x).
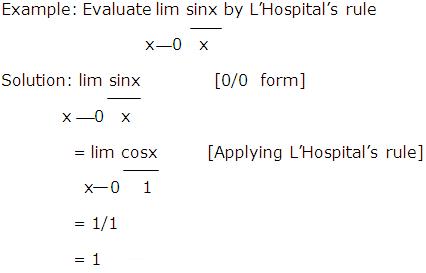
L’Hospital’s Rule for the form ∞/∞
Suppose that f and g are differentiable functions on an open interval containing x=a, except possibly at x=a, and that
![]()
If lim [f’(x)/g’(x)] has a finite limit, or if this limit is +∞ or -∞ then
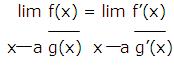
Moreover, this statement is also true in the case of a limit as x a-, x a+, x -∞ or as x +∞
Example: Apply L’Hospital’s rule and evaluate the following
![]()
Solution: The numerator and denominator both have a limt of +∞, so we have an indeterminate form of type ∞/∞. Applying L’Hospital’s rule,
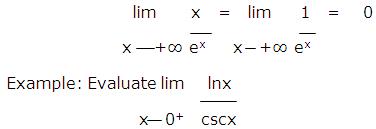
Example: Evaluate lim lnx
x 0+ cscx
Solution: The numerator has a limit of -∞ and the denominator has a limit of +∞, so we have an indeterminate form of type ∞/∞. Applying L’Hospital’s rule
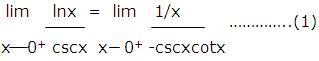
This last limit is again an indeterminate form of type ∞/∞. Moreover, any additional applications of L’Hospital’s rule will yield powers of 1/x in the numerator and expressions involving cscx and cotx in the denominator; thus, repeated application of L’Hospital’s rule simply produces new indeterminate forms. We must try something else. The equation (1) can be written as,
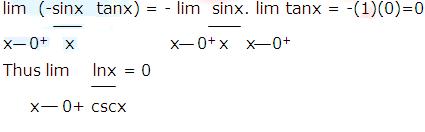
Indeterminate forms
There are some more other indeterminate forms other that 0/0 and ∞/∞ forms. We can discuss about them now.
In general, the limit of an expression that has one of the forms f(x)/g(x), f(x).g(x), f(x)g(x), f(x)-g(x), f(x)+g(x) is called indeterminate form if the limits of f(x) and g(x) individually exert conflicting influences on the limit of the entire expression.
For example ![]()
It is an indeterminate form of type 0.∞ because the limit of the first factor is 0 and the limit of the second factor is -∞ and these influences work together to produce a limit of -∞ for the product.
Indeterminate forms of 0.∞ can sometimes be evaluated by rewriting the product as a ratio and then applying L’Hospital’s rule for indeterminate forms of type 0/0 or ∞/∞.
Expressions of the form ∞-∞, 00, ∞0 and 1∞ are all indeterminate forms.
Cauchy Mean Value Theorem
Let f and g be continuous on [a, b] and differentiable on (a, b). Suppose that g’(x)≠0 for xЄ(a, b). Then there exists cЄ(a, b) such that
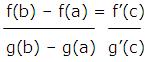
Examples:
Example: 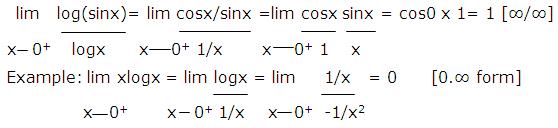
Example: Using Cauchy Mean Value Theorem, show that 1-(x2/2!) < cosx for x≠0
Solution: Apply Cauchy Mean Value Theorem f(x) = 1-cosx and g(x)=x2/2. We get ![]() for some c between 0 and x
for some c between 0 and x
Now try it yourself! Should you still need any help, click here to schedule live online session with e Tutor!
About eAge Tutoring:
eAgeTutor.com is the premium online tutoring provider. Using materials developed by highly qualified educators and leading content developers, a team of top-notch software experts, and a group of passionate educators, eAgeTutor works to ensure the success and satisfaction of all of its students.
Contact us today to learn more about our tutoring programs and discuss how we can help make the dreams of the student in your life come true!