Riemann Sum Approximation
The definite integral of a continuous function ‘f’ over an interval [a, b] is computed as a∫b f(x)dx = lim Σf(xk*)∆x, where the sum that appears on the right side is called Riemann sum. In this formula, the interval [a, b] is divided into n subintervals of width ∆x = (b-a)/n, and xk* denotes an arbitrary point in the kth sub-interval It follows that as n increases the Riemann sum will eventually be a good approximation to the integral, which we denote by writing
a∫b f(x)dx ≈ Σf(xk*)∆x
a∫b f(x)dx ≈ ∆x[f(x1*) + f(x2*) + …….+f(xn*)]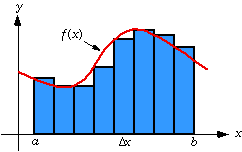
Here we denote the values of ‘f’ at the endpoints of the subintervals by
y0=f(a), y1=f(x1), y2=f(x2), ………, yn-1=f(xn-1), yn=f(b) and we will denote the values of f at the midpoints of the subintervals by ym1, ym2, ……ymn
Trapezoidal Approximation
The left-hand and right hand endpoint approximations are rarely used in applications; however, if we take the average of the left-hand and right hand endpoint approximations, we obtain a result, called the trapezoidal approximation, which is commonly used as,
a∫b f(x)∆x ≈ (b-a)/2n [ y0 + 2y1 + …..+ 2yn-1 + yn]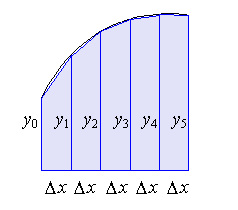
The name trapezoidal approximation can be explained by considering the case in which f(x)≥0 on [a, b], so that a∫b f(x)dx represents the area under f(x) over [a, b]. Geometrically, the trapezoidal approximation formula results if we approximate this area by the sum of the trapezoidal areas as shown in the figure
Left end point Approximation: The formula for evaluating left end point approximation is given by
a∫b f(x)dx = (b-a)/n [ y0 + y1 + ……….. + yn-1]
Right Endpoint Approximation: The formula for evaluating right end point approximation is given by
a∫b f(x)dx = (b-a)/n [y1 + y2 + …………. + yn]
Mid-Point Approximation: The formula for evaluating midpoint approximation is given by
a∫b f(x)dx = (b-a)/n [ym1 + ym2 + ………..+ ymn] where m1, m2 ……mn represents the mid values.
Example: Use Trapezoidal rule to approximate 0∫πsinx dx using n=10 sub intervals
Solution: a=0, b=π n=10 and f(x)=sinx, (b-a)/n = π/10
0∫π sinx dx = (π/20)[y0 + 2y1 + 2y2 + …………+2yn-1 + yn]
= (π/20) [ sin(0) + 2sin(π/10) + 2sin(2π/10) + ……..sin(10π/10)
= 1.983523538
Comparison of the Midpoint and Trapezoidal Approximations
The table below shows the comparison between midpoint and trapezoidal approximations for the function ln 2 = 1∫2(1/x)dx with n=10 subdivisions
Midpoint Approximation

1∫2 (1/x)dx = (0.1)(6.928353603) = 0.692835360
Trapezoidal Approximation
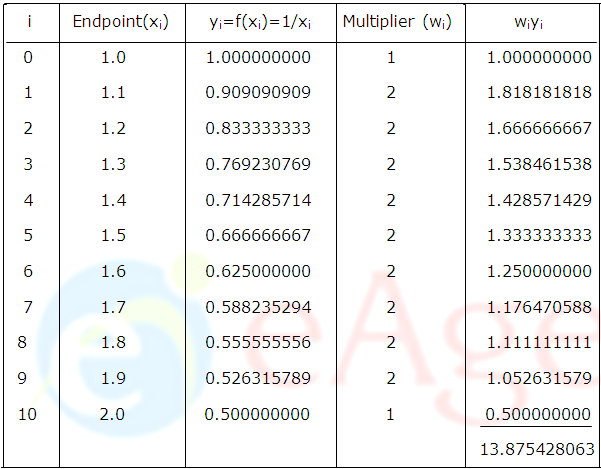
1∫2 (1/x)dx = (0.05)(13.875428063) = 0.693771403
The value of ln 2 is rounded to nine decimal places and we have seen that midpoint approximation produces a more accurate result than the trapezoidal approximation. Hence we can conclude that,
If f be a continuous on [a, b] and let |EM| and |ET| be the absolute errors that result from the midpoint and trapezoidal approximations of a∫bf(x)dx using n subintervals.
a) If the graph of f is either concave up or concave down on (a, b), then |EM|<|ET|, which means that the error from the midpoint approximation is less than from the trapezoidal approximation.
b) If the graph of ‘f’ is concave down on (a, b) then Tn <a∫b f(x)dx < Mn
c) If the graph of ‘f’ is concave up on (a,b), then Mn < a∫b f(x)dx < Tn
Simpson’s Rule
Simpson’s Rule is given by

Now try it yourself! Should you still need any help, click here to schedule live online session with e Tutor!
About eAge Tutoring:
eAgeTutor.com is the premium online tutoring provider. Using materials developed by highly qualified educators and leading content developers, a team of top-notch software experts, and a group of passionate educators, eAgeTutor works to ensure the success and satisfaction of all of its students.
Contact us today to learn more about our tutoring programs and discuss how we can help make the dreams of the student in your life come true!