Introduction

If ‘f’ has derivatives of all orders at x₀, then we call the series

The Taylor series for ‘f’ about x=x₀. 
In the special case where x₀=0, this series becomes

which is called as the Maclaurin series of ‘f’.
Note that the nth Maclaurin and Taylor polynomials are the nth partial sums for the corresponding Maclaurin and Taylor series.
Example: Find the Maclaurin series for 1/(1-x)
Solution: We know that the nth Maclaurin polynomial for 1/(1-x) is
p_n(x) = Σx^k = 1+x+x²+………+x^k (n=0, 1, 2………….)
Thus, the Maclaurin series for 1/(1-x) is
Σx^k= 1+x+x²+x³+…….+x^k+…………..
Example: Find the Taylor series for 1/x about x=1
Solution: We know that the nth Taylor polynomial for 1/x about x=1 is
Σ(-1)^k(x-1)k=1-(x-1)+(x-1)²-(x-1)³+….+(-1)ⁿ(x-1)ⁿ
Thus the Taylor series for 1/x about x=1 is
Σ(-1)^k(x-1)k=1-(x-1)+(x-1)²-(x-1)³+……..+(-1)^k(x-1)^k+……….

Power Series in x

Maclaurin and Taylor series differ from the series that we have discussed above that their terms are not merely constants, but instead involve a variable.  These are examples of power series which is defined as
If c₀, c₁, c₂, ……. Are constants and x is a variable then a series of the form
        Σckxk= c₀+c₁x+c₂x²+………..+c_kx^k+……………….. is called a power series in x
Here are some examples

Indeed every Maclaurin series is a power series in x.

Radius and interval of convergence

If a numerical value is substituted for x in a power series Σc_kx^k, then the resulting series of numbers may either converge or diverge.  This leads to the problem of determining the set of x-values for which a given power series converges; this is called its convergence set.
For any a power series in x, exactly one of the following is true:
a)    The series converges only for x=0
b)    The series converges absolutely (and hence converges) for all real values of x
c)    The series converges absolutely (and hence converges) for all x in some finite open interval (-R, R) and diverge if x<-R or x>R.  At either of the values x=R or x=-R, the series may converge absolutely, converge conditionally or diverge, depending on the particular series.
This theorem states that the convergence set for a power series in x is always as interval centered at x=0 (possibly just the value x=0 itself or possibly infinite).  For this reason, the convergence set of a power series in x is called the interval of convergence.  In the case where the convergence set is the single value x=0 we say that the series has radius of convergence 0, in the case where the convergence set is (-∞, +∞) we say that the series has radius of convergence +∞ and in the case where the convergence set extends between –R and R we say that the series has radius of convergence R.    

The usual procedure for finding the interval of convergence of a power series is to apply the ratio test for absolute convergence.  The following example illustrates how this works.
Example: Find the interval of convergence and radius of convergence of the following power series Σx^k and Σx^k/k!

Solution:
Σx^k
We apply the ratio test for absolute convergence.  We have
            
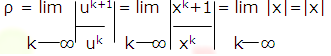
So the series converges absolutely if ρ = |x| <1 and diverges if ρ=|x|>1.  The test is inconclusive if |x|=1 (x=1 or x=-1), which means that we will have to investigate convergence at these values separately.  At these values the series becomes
               Σ1^k = 1 + 1+ 1+ 1+ 1+………… [x=1]
               Σ(-1)^k = 1-1+1-1+1-1+……..[x=-1]
Both of which diverge, thus, the interval of convergence for the given power series is (-1, 1) and the radius of convergence is R=1.

Σx^k/k!
Applying the ratio test for absolute convergence, we obtain
  

Power Series in x-x0

Σc_k(x-x₀)^k = c₀+c₁(x-x₀)+c₂(x-x₀)²+…..+c_k(x-x₀)^k+…… is called a power series in x-x₀.
For a power series Σc_k(x-x₀)^k, exactly one of the following statements is true:
a)    The series converges only for x=x₀.
b)    The series converges absolutely and hence converges for all real values of x.
c)    The series converges and hence converges for all x in some finite open interval (x₀-R, x₀+R) and diverges is x<x₀-R or x>x₀+R.  At either of the values x=x₀-R or x=x₀+R, the series may converge absolutely, converge conditionally or diverge depending on the particular series.
It follows from the above statements that the set of values for which a power series in x-x₀ converges is always an interval centered at x=x₀; we call this the interval of convergence.  In part (a) the interval of convergence reduces to the single value x=x₀ in which case we say that the series has radius of convergence R=0; in part (b) the interval of convergence is infinite, in which case we say that the series has radius of convergence R=+∞; and in part (c) the interval extends between x₀-R and x₀+R, in which case we say that the series has radius of convergence R.
                                                                      
Now try it yourself!  Should you still need any help, click here to schedule live online session with e Tutor!

About eAge Tutoring:

eAgeTutor.com is the premium online tutoring provider.  Using materials developed by highly qualified educators and leading content developers, a team of top-notch software experts, and a group of passionate educators, eAgeTutor works to ensure the success and satisfaction of all of its students.  

Contact us today to learn more about our tutoring programs and discuss how we can help make the dreams of the student in your life come true!

Reference Links:

• http://en.wikipedia.org/wiki/Taylor_series
• http://www.intmath.com/series-expansion/2-maclaurin-series.php
• http://en.wikipedia.org/wiki/Power_series
• http://en.wikipedia.org/wiki/Radius_of_convergence