Argand Plane
We have already learned that corresponding to each ordered pair of real numbers (x, y) we get a unique point in XY plane with reference to a set of mutually perpendicular lines known as X-axis and Y-axis. The complex number z=x + iy which corresponds to the ordered pair (x, y) can be represented geometrically as the unique point P(x, y) in the XY plane.
The plane having a complex number assigned to each of its point is called the Complex Plane or Argand Plane.
The point on x-axis corresponds to the complex numbers of the form a+i0 and the point on the y-axis corresponds to the complex numbers of the form 0 + ib.
The x-axis is called as real axis and y-axis is called as imaginary axis in the Argand Plane.
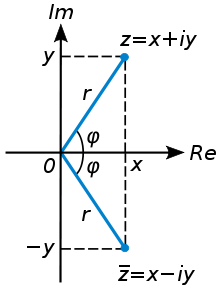
The representation of a complex number z=x + iy and its conjugate z= x- iy in the Argand Plane are respectively the points (x, y) and (x, -y). Clearly (x, -y) is the mirror image of the point (x, y) on the real axis.
In the Argand Plane, the modulus of a complex number x + iy = √x2 + y2 is the distance between the point P(x, y) and the origin O(0, 0).
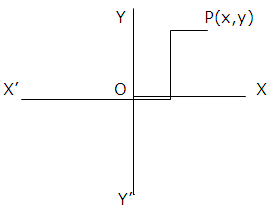
Here OP = √x2+y2
Polar Representation of a Complex Number
Let the point P represent the non-zero complex number z = x +iy. Let the modulus of z be r and θ be the angle made by OP with positive direction of x-axis. Then we can note that the point P is determined by the ordered pair (r, θ), called the polar co-ordinates. Here we consider the origin as the pole and the positive x-axis as the initial line.
So, we have, x = rcosθ and y = rsinθ and hence z = x + iy becomes z=r(cosθ +isinθ), which is called polar representation of the complex number z
Here r=|z|=√x2+y2 and the value of θ lies between 0 and 2π which is called as argument or amplitude of z and is denoted by argz.
In other words, if z=x + iy is a complex number then its polar form is given by z=r(cosθ + isinθ), where ‘r’ is the modulus and θ is the amplitude or argument.
Easy method for finding the argument, θ
We can easily find the modulus ‘r’ but the value of ‘θ’ varies according to the different quadrants. While finding the value of ‘θ’, we must be aware of the standard angles and its values otherwise we find it difficult.
Let θ be the standard angle, if it comes in first quadrant then we can directly substitute its value. In other cases, we have to transform it to the corresponding standard value which we have learned in class XI. To overcome this difficulty here are some formulas to find the argument ‘θ’
If ‘θ’ lies in first quadrant take θ = θ
Second quadrant, θ = π-θ
Third quadrant, θ = - (π-θ)
Fourth quadrant, θ = -θ
Below given are few examples
1. Convert √3+i in the polar form
Let z= x + iy = √3 +i
We know x=√3 and y=1
Again we have r=√(√3)2 + 12
= 2
rcosθ = √3 and rsinθ = 1
2cosθ=√3 and 2sinθ = 1
Cosθ = √3/2 and sinθ = ½
Both cosθ and sinθ are positive, so ‘θ’ belongs to 1st quadrant.
The value of ‘θ’ for which cosθ=√3/2 and sinθ=1/2 is 30˚ or π/6
Hence r=2 and θ=π/6
Polar form of √3+i = 2[cosπ/6 + isinπ/6]
2. Find the modulus and argument of the complex number -1-i
Let z= x +iy = -1-i
x=-1 and y=-1
r= √x2+y2 = √(-1)2+(-1)2
= √1+1 =√2
Modulus, r= √2
Here √2 cosθ= -1 and √2 sinθ = -1
Cosθ =-1/√2 and sinθ=-1/√2
Both cosθ and sinθ are negative, so θ belongs to third quadrant.
The value of θ for which cosθ = sinθ =1/√2 is π/4 [without sign]
Hence the argument = - (π-θ) = - (π-π/4) = ![]()
Argument = 3π/4
Fundamental theorem of Algebra
Fundamental theorem of Algebra states that “A polynomial equation of degree n has n roots”
The above statement tells us that a linear equation has one root, quadratic equation has two roots, cubic equation has three roots, fourth degree equation has four roots and so on.
Quadratic Equations
We know that the general quadratic equation is of the form ax2+bx+c=0, a≠0. This equation has two roots and the nature of roots has been studied in earlier classes. Here we consider the case where the discriminant, b2-4ac<0.
We have learned that square root of negative real numbers is set of complex numbers, therefore, the solution of ax2+bx+c=0 is given by

Now try it yourself! Should you still need any help, click here to schedule live online session with e Tutor!
About eAge Tutoring:
eAgeTutor.com is the premium online tutoring provider. Using materials developed by highly qualified educators and leading content developers, a team of top-notch software experts, and a group of passionate educators, eAgeTutor works to ensure the success and satisfaction of all of its students.
Contact us today to learn more about our tutoring programs and discuss how we can help make the dreams of the student in your life come true!