Shortest Distance (Introduction)
 If two lines intersect in space at a point, then the shortest distance between them is zero. If two lines in space are parallel, then the shortest distance between them will be the perpendicular distance which means that the length of perpendicular drawn from a point on one line onto to the other line. If the lines are neither intersecting nor parallel then the shortest distance in the perpendicular distance between them.
If two lines intersect in space at a point, then the shortest distance between them is zero. If two lines in space are parallel, then the shortest distance between them will be the perpendicular distance which means that the length of perpendicular drawn from a point on one line onto to the other line. If the lines are neither intersecting nor parallel then the shortest distance in the perpendicular distance between them.
Skew Lines
The lines which are neither intersecting nor parallel are called skew lines. Such pair of lines are non-coplanar. For skew lines, the line of shortest distance will be perpendicular to both the lines.
Distance between two skew lines
Vector Form: If r=a1+λb1 and r=a2+μb2 are the vector equations of two lines then, the shortest distance between them is given by
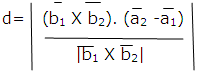
Cartesian Form: 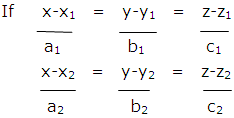
are the Cartesian equations of two lines, then the shortest distance between them is given by
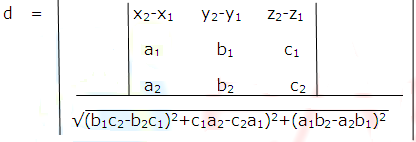
Distance between parallel lines
If ![]() are the vector equations of two parallel lines then shortest distance between them is given by
are the vector equations of two parallel lines then shortest distance between them is given by
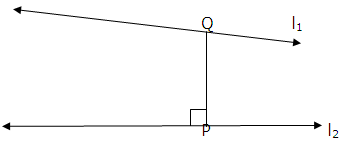
Perpendicular distance of a point from a line
For finding the perpendicular distance of a point from a line, first we have to find the coordinates of the foot of perpendicular. After getting the coordinates of foot, we can calculate the distance using distance formula.
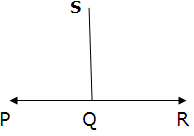
In the adjoining figure, first we have to find the coordinates of Q. We know ‘S’, using the coordinates of Q and S we can find the distance QS [Distance formula]
Example: Find the shortest distance between the lines
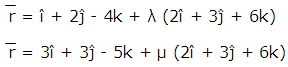
Solution: The given lines are parallel, so a1 = î + 2ĵ - 4k, a2 = 3î + 3ĵ - 5k and b = 2î + 3ĵ + 6k
Hence, 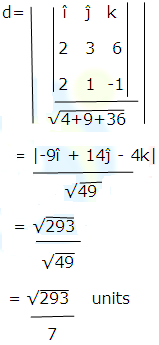
Now try it yourself! Should you still need any help, click here to schedule live online session with e Tutor!
About eAge Tutoring:
eAgeTutor.com is the premium online tutoring provider. Using materials developed by highly qualified educators and leading content developers, a team of top-notch software experts, and a group of passionate educators, eAgeTutor works to ensure the success and satisfaction of all of its students.
Contact us today to learn more about our tutoring programs and discuss how we can help make the dreams of the student in your life come true!