To make calculations easier, we have few rules or laws of exponents:
•    Multiplying Powers with the same base
•    Dividing Powers with the same base
•    Power with Exponent zero
•    Power of a Power
•    Multiplying Powers with the same exponents
•    Dividing Powers with the same exponents

Let’s discuss each one of them in detail:

Law 1: Multiplying Powers with the same base

If ‘a’ is any non – zero rational number and m, n are natural numbers, then
a^m x aⁿ = a^{m + n}

Also, If ‘a’ is any non – zero rational number and m, n, p are natural numbers, then
a^m x aⁿ x a^p = a^{m + n + p}

Example: Simplify: 3² x 3⁵
= 3^{2 + 5}
= 3⁷

Law 2: Dividing Powers with the same base

If ‘a’ is any non – zero rational number and m, n are natural numbers such that m > n, then
                                                                               a^m ÷ aⁿ = a^{m – n} or a^m = a^{m – n}
                                                                                                          aⁿ

Example: Simplify: 9¹² ÷ 9¹⁰
= 9^{12 – 10}
= 9²

Law 3: Power with exponent zero

If ‘a’ is any non – zero rational number raise to power 0, then it is equal to 1
a⁰ = 1

Example: 7³ ÷ 7³
= 7^{3 – 3}
= 7⁰
= 1

Law 4: Power of a Power

If ‘a’ is any rational number different from zero and m, n are natural numbers, then
(a^m)ⁿ = a^{m x n} = (aⁿ)^m

Example: Simplify: (2³)⁴ = 2^{3 x 4} = 2¹²

Law 5: Multiplying Powers with the same exponents

If a, b are non – zero rational numbers and n is a natural number, then
aⁿ x bⁿ = (ab)ⁿ

Also, If a, b, c are non – zero rational numbers and n is a natural number, then
aⁿ x bⁿ x cⁿ = (abc)ⁿ

Example: 2⁵ x 3⁵
= (2 x 3)⁵
= 6⁵

Law 6: Dividing Powers with the same exponents

If a and b are non – zero rational numbers and n is a natural number, then
                                                                                              aⁿ = a ⁿ
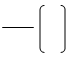                                                                               bⁿ = b

Example: (2/3)²
= (2 x 2)/(3 x3)
= 4/9
       

Now try it yourself!  Should you still need any help, click here to schedule live online session with e Tutor!

About eAge Tutoring:

eAgeTutor.com is the premium online tutoring provider.  Using materials developed by highly qualified educators and leading content developers, a team of top-notch software experts, and a group of passionate educators, eAgeTutor works to ensure the success and satisfaction of all of its students.

Contact us today to learn more about our tutoring programs and discuss how we can help make the dreams of the student in your life come true!

Reference Links:

•     http://en.wikipedia.org/wiki/Exponentiation
•     http://en.wikipedia.org/wiki/Natural_number
•     http://en.wikipedia.org/wiki/Rational_number