English Guide: Practical Tips for Better English Communication
A rich vocabulary is an important indicator of a person’s command over the English language. That is one of the reasons why we keep offering tips regularly on how to improve your English vocabulary. However, building one’s vocabulary requires sustained effort to discover and add new words that can be used effectively in your communication.
The process of enriching one’s vocabulary can be simplified into 4 key steps: read a lot of good English books,...
The last two decades have been hugely transformational as digital technologies have disrupted every walk of life. This will only continue in the new decade, as machine learning, deep learning and artificial intelligence (AI) begin to play an integral part in our workplaces. As a result, workplaces will require very different skillsets than they needed until now. If you are a youngster looking for rapid career development in this new decade, then...
If you are planning to study, work or even immigrate to any western country (Australia, New Zealand, US, Canada, UK – to name a few), you will most likely be required to get a good IELTS score to get the requisite entry visa. Typically, this means that you should get a score of band 7 or higher to maximise the chances of getting the visa approval. The IELTS score contributes significant points to the points-system used by many countries for...
Recently, the former Union Minister and former top UN diplomat Mr.Shashi Tharoor was asked the secret of his exceptional English vocabulary. While he joked initially, he then gave the secret of his amazing and enviable vocabulary: Reading. Yes, the open secret to a strong and deep English vocabulary is as simple as that- a lot of reading of good English books.
Mr.Tharoor dispelled the notion that he moves around carrying an English dictionary....
Emotional intelligence (used interchangeably with emotional quotient) and social awareness are increasingly important attributes that have a bearing on how one is perceived in a social or professional environment. The words and phrases we use are manifestations of our social awareness and therefore, require careful thought. Following are 5 English phrases that people avoid for their likelihood of being misinterpreted.
We list below five of...
You can find your dream job on Jooble
If you are like most people, you would like to achieve professional growth and success in your career. Typically, career success would mean promotions, greater responsibilities and accompanying financial rewards. If you look around you, you will often find that the people who progress and move up the ladder are those who demonstrate passion at work, are proactive, and of course, perform on the job at hand...
It is never a pleasant task to call up the customer service of one of your service providers and complain about any issue you may have encountered, whether it is a faulty bill or inadequate service you have received. Nevertheless, making unpleasant telephone conversations to lodge a complaint is a part of life that one must be prepared for. How you go about making this conversation can go a long way in determining whether you get the desired...
Let us say that your current English speaking skills aren’t great. You aren’t very confident of being able to communicate confidently and effectively in English with anyone, be it a small group or a large one. However, you are very determined to improve your spoken English skills rapidly and prove to yourself that you can do it, while making a good impression on those around you. Taking up an English speaking course is obviously one way to...
If you are planning to take the IELTS test, you would be aware that the test comprises of four different modules: Listening, Reading, Writing and Speaking. For many IELTS test takers, the speaking test is often the most difficult. This is not very surprising because it is akin to speaking in public. It is a known fact that ‘public speaking’ is one of the scariest tasks for people.
There are three sections in the speaking test in IELTS. The...
There is a quote attributed to the writer Stephen King that says that “if you want to be a writer, there are two things you must do: Read a lot and write a lot.” You can extend that quote to say the following: “To be a fluent English speaker, you must listen a lot and speak a lot.” While there is no substitute to this mantra, we will give you some more details of how you could work towards becoming a more fluent speaker.
To start with, let’s...
It is well known that the quality of communication between two or more individuals, impacts the outcome of business meetings. While the exact content of the meeting and its structure are critical, certain external factors like the energy and enthusiasm of the participants in a meeting, also play a very important role in the success or failure of a meeting. In this article, we will offer some simple tips on how you can improve the chances of a...
A career in sales can be very exciting and lucrative for people who do well in it. Sales brings in revenues for any organisation, and revenues help companies move forward. As long as one is performing well and continues to bring in sales, one’s job is fairly secure because in times of adversity businesses slash costs, while trying to keep revenues high. Yet, success in a sales career isn’t guaranteed for everyone. It takes certain personality...
When it comes to learning spoken English, many people often mistake the purpose of the learning. They tend to think that acquiring English speaking skills is about speaking with a British or American accent. They couldn’t be farther from truth. The true purpose should be to learn to speak English correctly, fluently, confidently and in manner that the listener understands the communication without much difficulty.
Too much emphasis is laid on...
In a recent article, we wrote about the difference between improve and improvise and how to use these two similar terms appropriately. Continuing this series on using similar-sounding English words correctly, let us consider the use of the words “affect” and “effect”.
Both terms mean “impact” or “result” of something, but their usage varies depending on the context in which they are being used.
Affect
The word “affect” is generally used in the...
English language has plenty of words that seem very similar but mean very different. It is quite easy to ignore the subtle difference in the words themselves and consider them to mean the same thing. This results in incorrect usage of the words when writing or speaking in English, which may confuse the listener or create a negative impression about your English Communication skills. Let’s focus on two words, improve and improvise; the former is a...
Someone has rightly said, “In the mundane, nothing is sacred. In sacredness, nothing is mundane.”
Mundane is boring. There comes a time when you feel saturated with the routine tasks you are doing and you feel like doing different and challenging things. Your ardent desire to take up additional work and prove your worth overwhelms you. But this needs to be communicated effectively to your boss. Your boss should be aware that you are geared up...
Gratitude is of vital importance in human life. We need to thank people who have, directly or indirectly, explicitly or implicitly, made a positive change in our life. ‘Thank You’ is the least that we can say. So never shy away from that.
In professional life too, gratefulness is of utmost importance, especially when someone has helped you climb up the career ladder.
It’s your promotion party and you have to give a thank you speech – this...
We all have encountered situations wherein there were unavoidable or unforeseen circumstances because of which we had to extend our leave. For example, sickness, family issues, marriage etc. Now here comes the uncomfortable question – how to ask the boss for a leave extension. Quite tricky, huh?
When you are already on leave and then you have to request for extension of leave, it should be done in such a way that it is granted without much...
A few months back, a video of a job prospect venting out his frustrations on having to speak in English at job interviews, went viral. The protagonist of the video, a youngster, who could speak English fluently was angry that he was always asked to speak in English, and he let out his frustration with a series of expletives in Hindi. The fact that the video went viral and was shared by a large audience in the country, especially among...
Man is a social animal. We cannot survive in isolation. Also, we all crave for love and attention, no denying that. We are constantly expanding our social network. Be it personal or professional life, networking is of utmost importance to us: Social networking, for getting love and affection, and professional networking for career enhancement.
In this competitive world, we cannot lounge around waiting for opportunities to knock at our door. We...
Someone has rightly said, “Good conversation starts with good listening”. Our teachers have often told us that we wouldn’t learn anything new from talking but we will definitely learn something new from listening. How true!
There’s a lot of buzz about spoken English these days, but people tend to forget that English listening is also an integral and inseparable part of English communication, which cannot be overlooked.No wonder then the...
India is undergoing a digital revolution. The country has embarked on the ‘Digital India’ movement that has been officially promoted by the Indian government. It is therefore not surprising to see a jump in career opportunities in the field of digital marketing, especially search engine marketing (SEM). This field attracts a lot of freshers and young job aspirants. Having good English skills will enable a person to take advantage of the growing...
Good manners will open doors that the best education cannot.”
Etiquette is the science of living. It embraces everything.People all over the world are judged, liked, disliked, remembered or looked down with contempt based on their manners. Good manners speak a lot about your personality.
It is imperative that you display your best behaviour when you are in a public place especially when eating out. When you walk into a restaurant you don’t want to...
Good teamwork is essential not only for the growth of any organisation but also for the personal growth of individuals in the organisation. An essential component of achieving good team bonding is when team members express positive thoughts about fellow team members to them directly. Sincere compliments and praise go a long way in making a person feel good and feel motivated to perform better for the team and the organisation.
There are a...
At the outset, let us state that we hope you never have to apply for a compassionate leave. However, the reality is that most of us, at some stage of our life, end up having to request for such leaves. This article is written to specifically help you in case of such an eventuality.
Before we get into the mechanics of applying for compassionate leave, let us first understand what is compassionate leave. It is leave granted to an employee upon death...
Solution of a Linear Equation
Solving a linear equation means determining it roots.
Three methods of solving a linear equation:
a) Trial and Error method.
b) Systematic method.
c) Transposition method.
Let’s go through each of the method one by one.
Trial and Error method
In this method, we often make a guess of the root of the equation. We find the values of L.H.S. and R.H.S. of the given equation for different values of the variable. The value of the variable for which L.H.S. = R.H.S. is the root of the equation.
Example: Solve x + 7 = 10 by the trial and error method.
We first evaluate the L.H.S. and R.H.S. of the given equation for some values of x and continue to give new values till the L.H.S. becomes equal to the R.H.S.
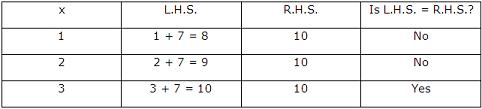
Clearly, L.H.S. = R.H.S. for x = 3. Hence, x = 3 is the solution of given equation.
Systematic method
In this method, we solve the equation by using the following rules:
Rule 1 – Same quantity (number) can be added to both sides of an equation without changing the equality.
Rule 2 – Same quantity (number) can be subtracted from both sides of an equation without changing the equality.
Rule 3 – Both sides of an equation may be multiplied by the same non – zero number without changing the equality.
Rule 4 - Both sides of an equation may be divided by the same non – zero number without changing the equality.
Example: Solve the equation: X/5 + 11 = 1/15.
We have, X/5 + 11 = 1/15
X/5 + 11 – 11 = 1/15 -11
X/5 = 1/15 – 11
X/5 = (1 – 165)/15
X/5 = -164/15
5 x X/5 = 5 x -164/15
X = -164/3
Thus, X = -164/3 is the solution of the given equation.
Transposition method
The transposition method involves the following equation:
Step 1 – Obtain the linear equation.
Step 2 – Identify the variable (unknown quantity) and constants (numerals).
Step 3 – Simplify the L.H.S. and R.H.S. to their simplest forms by removing brackets.
Step 4 – Transpose all terms containing variable on L.H.S. and constant terms on R.H.S. Note that the sign of the terms will change in shifting them from L.H.S. to R.H.S. and vice versa.
Step 5 – Simplify L.H.S. and R.H.S. in the simplest form so that each side contains just one term.
Step 6 – Solve the equation obtained in Step 5 by dividing both sides by the coefficient of variable on L.H.S.
Example: Solve: X/2 – 1/5 = X/3 + 1/4
We have, X/2 – 1/5 = X/3 + 1/4
The denominators on two sides are 2, 5, 3 and 4.Their L.C.M. is 60.
Multiplying both sides of the given equation by 60, we get
60 (X/2 – 1/5) = 60 (x/3 +1/4)
60 x X/2 – 60 x 1/5 = 60 x X/3 + 60 x 1/4
30X -12 = 20X + 15
30X – 20X = 15 + 12 [On transposing 20X to L.H.S. and -12 to R.H.S.]
10X = 27
X = 27/10
Hence, X = 27/10 is the solution of the given linear equation.
Try these questions now:
1. 1/3x – 5/2 = 6 (Answer: x = 5/2)
2. x +7 -8x/3 = 17/6 – 5x/8 (Answer: x = 4)
Now try it yourself! Should you still need any help, click here to schedule live online session with e Tutor!
About eAge Tutoring :
eAgeTutor.com is the premium online tutoring provider. Using materials developed by highly qualified educators and leading content developers, a team of top-notch software experts, and a group of passionate educators, eAgeTutor works to ensure the success and satisfaction of all of its students.Contact us today to learn more about our guaranteed results and discuss how we can help make the dreams of the student in your life come true!
Reference Links :
Categories
Archives
- ► 2020 (2)
- ► 2019 (11)
- ► 2018 (44)
- ► 2017 (72)
- ► 2016 (150)
- ► 2015 (151)
- ► 2014 (197)
- ► 2013 (198)
- ► 2012 (49)
- ► 2011 (406)
- ► 2006 (10)
- ► 0000 (4)
Blog Subscription
Most Read Blog Posts
- How to Write a Formal Email Regarding a Leave/ Off?
- How to Describe Your Family?
- How to Describe your Home?
- How to Greet your Boss/ People in Office?
- How to Seek Appointment with your Doctor’s Receptionist?
- How to Describe a Restaurant to Your Friend?
- How to Describe your Phone and its Features?
- How to express likes and dislikes?
- How to describe your favourite movie?
- How to Describe Your City?
Recent Blog posts
- Improve your English vocabulary by learning root words
- Essential skills for the workplace in the 2020s
- How to score band 7 and above in IELTS?
- Voracious reading: The real secret to building a strong English Vocabulary
- 5 English phrases to avoid in conversation and display greater social awareness
- Communicate your passion at work for career success
- How to improve your spoken English fluency
- How to lodge a telephonic complaint against a faulty bill
- How to communicate with energy for more effective meetings
- To speak good English, surround yourself by people who speak English fluently
Find Us on Facebook
Find Us on Twitter
Find Us on Google Plus
Find Us on Youtube
Find Us on Linkedin